Свободные колебания консольной открытой цилиндрической оболочки
Цель: Модальный анализ консольной открытой цилиндрической оболочки.
Файл с исходными данными: 5.9.spr
Формулировка задачи: Определить собственные формы и частоты колебаний ω консольной открытой цилиндрической оболочки с плотностью материала ρ.
Ссылки: Olson M. D., Lindberg G. M., Vibration analysis of cantilevered curved plates using a new cylindrical shell finite element, Second conference on matrix methods in structural mechanics at Wright – Patterson Air Force Base in Ohio, AFFDL-TR-68-155, 1969, p. 247-269.
Исходные данные:
| E = 30.0·106 PSI = 2.0685·108 кПа | - модуль упругости; |
| ν = 0.3 | - коэффициент Пуассона; |
| ρ = 0.28386 lb/in3 = 7.8572 т/м3 | - плотность материала; |
| h = 0.12 in = 3.048·10-3 м | - толщина цилиндрической оболочки; |
| R = 24 in = 0.6096 м | - радиус срединной поверхности цилиндрической оболочки; |
| L = 12 in = 0.3048 м | - длина образующей цилиндрической оболочки; |
| W =12 in = 0.3048 м | - длина дуги направляющей цилиндрической оболочки. |
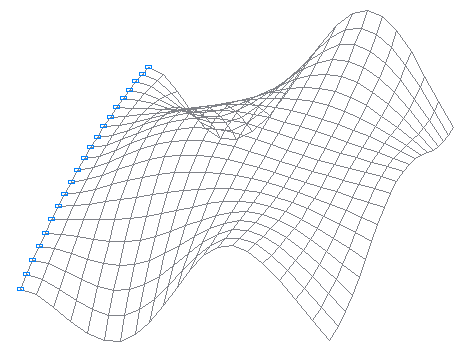
Конечноэлементная модель: Расчетная схема – система общего вида, 400 четырехузловых элементов оболочки типа 50. Сетка конечных элементов разбита с шагом 0.01524 м (20 элементов) в меридиональном направлении и в окружном направлении. Обеспечение граничных условий на защемленном криволинейном торце достигается за счет наложения связей по направлениям всех линейных и угловых перемещений (степени свободы X, Y, Z, UX, UY, UZ). Распределенная масса задается преобразованием статической нагрузки от собственного веса цилиндрической оболочки: ow = γ∙h, где γ = ρ∙g = 77.0791 кН/м3. Количество узлов в расчетной схеме – 441. Определение собственных форм и частот выполнено методом Ланцоша. При расчете используется согласованная матрица масс.
Результаты решения в SCAD
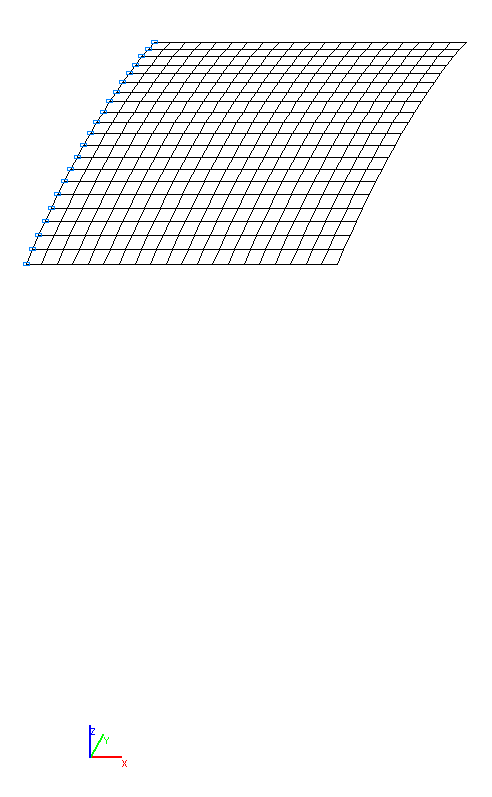

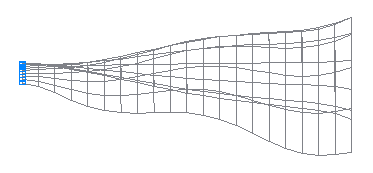
Расчетная схема


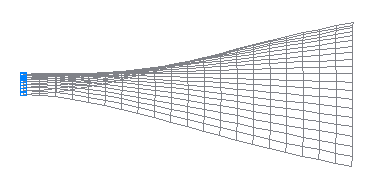
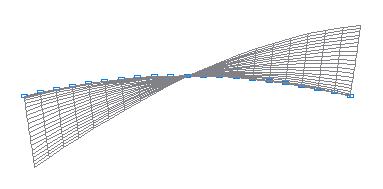
1-я собственная форма колебаний



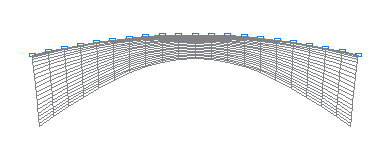
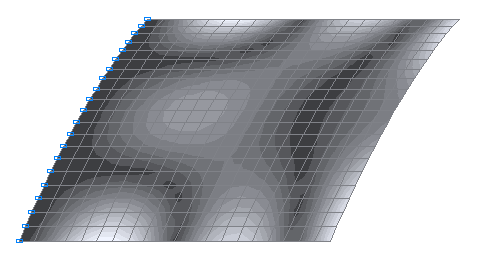
2-я собственная форма колебаний


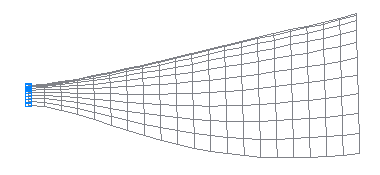

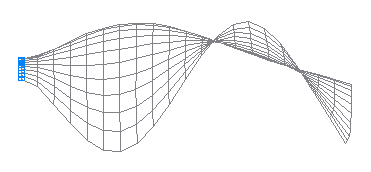
3-я собственная форма колебаний


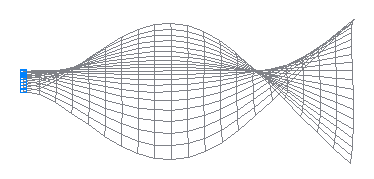
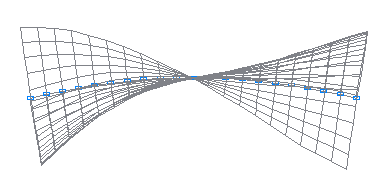
4-я собственная форма колебаний
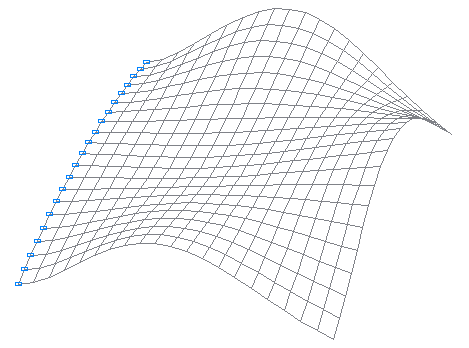

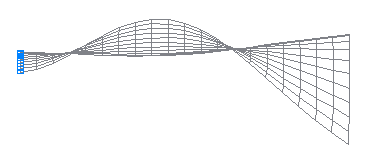
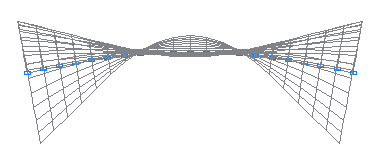
5-я собственная форма колебаний


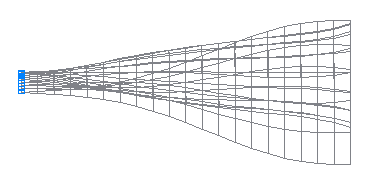
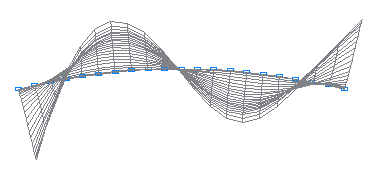
6-я собственная форма колебаний
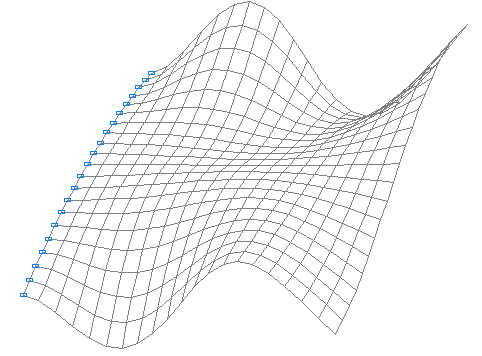
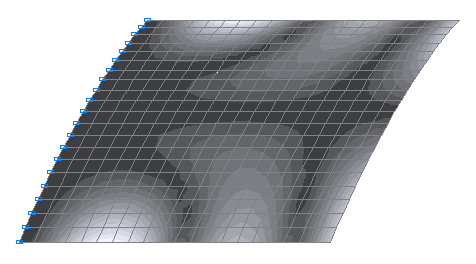
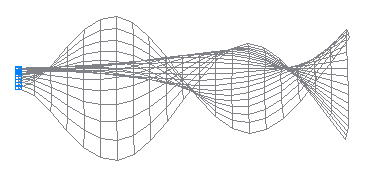
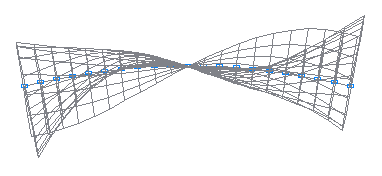
7-я собственная форма колебаний
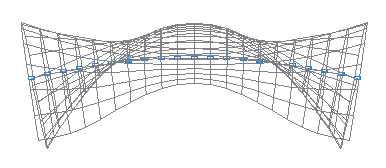
8-я собственная форма колебаний
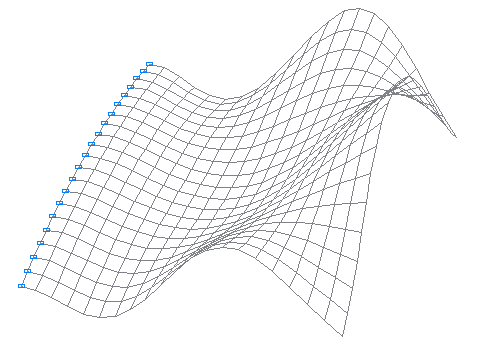

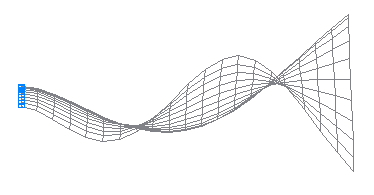
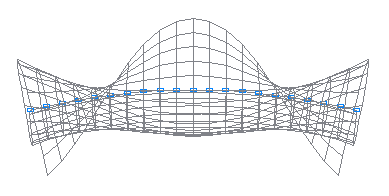
9-я собственная форма колебаний


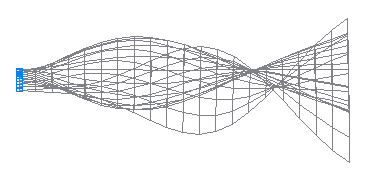
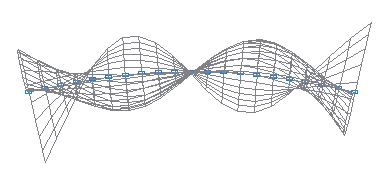
10-я собственная форма колебаний
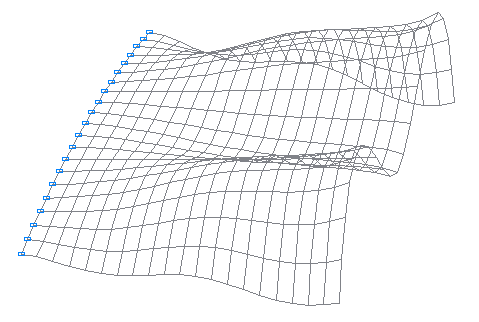

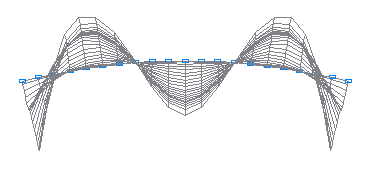
11-я собственная форма колебаний
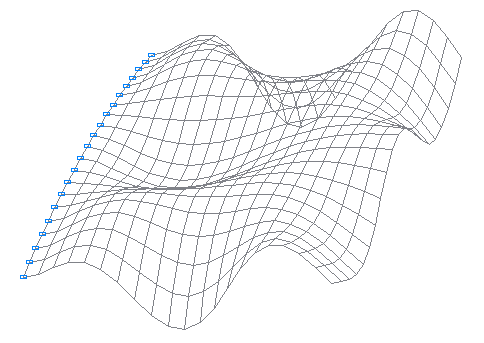

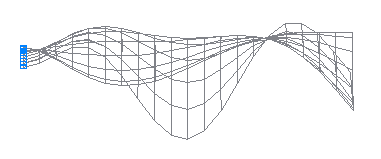
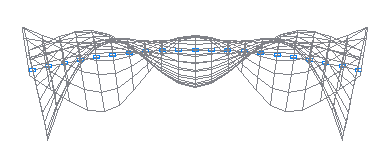
12-я собственная форма колебаний
Сравнение решений:
Собственные частоты колебаний ω, Гц
|
Форма колебаний |
Узловые линии |
Эксперимент |
SCAD |
Отклонения, % |
|---|---|---|---|---|
|
1 |
|
85.6 |
86.2 |
0.35 |
|
2 |
|
135.5 |
139.2 |
0.57 |
|
3 |
|
258.9 |
248.2 |
0.95 |
|
4 |
|
350.6 |
344.2 |
0.75 |
|
5 |
|
395.2 |
388.2 |
0.89 |
|
6 |
|
531.1 |
529.9 |
1.39 |
|
7 |
|
743.2 |
730.9 |
1.33 |
|
8 |
|
751.2 |
732.9 |
1.22 |
|
9 |
|
792.1 |
776.5 |
0.87 |
|
10 |
|
809.2 |
805.4 |
1.21 |
|
11 |
|
996.8 |
999.1 |
1.97 |
|
12 |
|
1215.0 |
1210.5 |
1.85 |












