Консольная балка под действием сосредоточенной поперечной силы
Цель: Определение деформированного состояния консольной балки от воздействия сосредоточенной поперечной силы.
Файлы с исходными данными:
| CS06_c_v11_3.spr | Стержневая расчетная модель |
| CS06_p_v11_3.spr | Плосконапряженная расчетная модель |
Формулировка задачи: Консольная балка прямоугольного сечения нагружается на свободном торце сосредоточенной поперечной силой Р. Определить перемещение z свободного торца балки с учетом влияния поперечного сдвига.
Исходные данные:
| E = 3.0·107 Па | - модуль упругости, |
| ν = 0.0 | - коэффициент Пуассона, |
| L = 10.0 м | - длина балки; |
| t = 0.1 м | - ширина поперечного сечения балки; |
| h = 1.0 м | - высота поперечного сечения балки; |
| k = 1.2 | - коэффициент сдвига; |
| P = 1.0 Н | - значение сосредоточенной силы |
Конечноэлементная модель: Рассматриваются две расчетные модели:
Стержневая модель (С), расчетная схема – плоская рама, 10 элементов типа 10. Сетка конечных элементов разбита по длине продольной оси с шагом 1.0 м. Обеспечение граничных условий на защемленном торце достигается за счет наложения связей по направлениям степеней свободы: X, Z, UY. Количество узлов в расчетной схеме – 11.
Плосконапряженная модель (П), 10 восьмиузловых элементов типа 30. Сетка конечных элементов разбита по длине продольной оси с шагом 1.0 м. Обеспечение граничных условий на защемленном торце достигается за счет наложения связей по направлениям степеней свободы: X, Z. Количество узлов в расчетной схеме – 53.
Результаты решения в SCAD

Расчетная схема. Стержневая модель
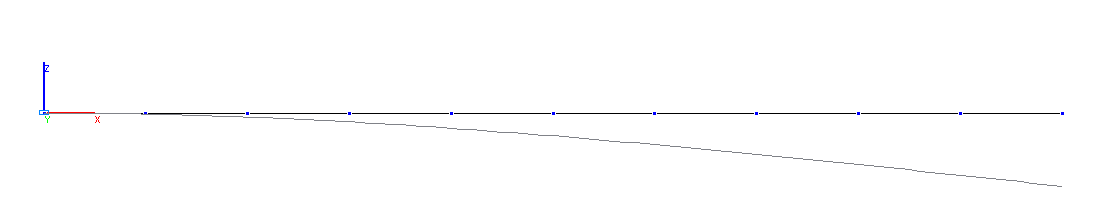
Деформированная схема. Стержневая модель

Перемещения z (м). Стержневая модель
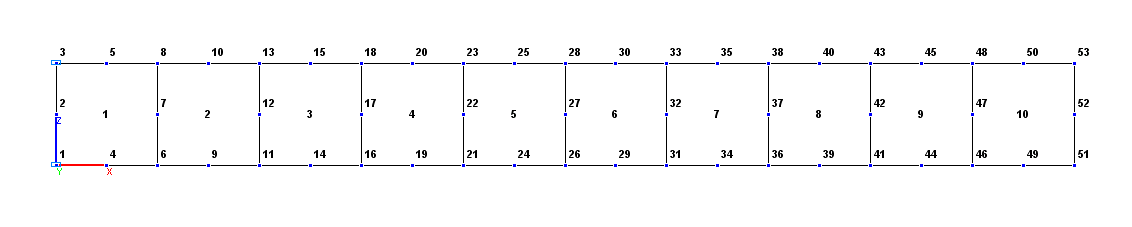
Расчетная схема. Плосконапряженная модель
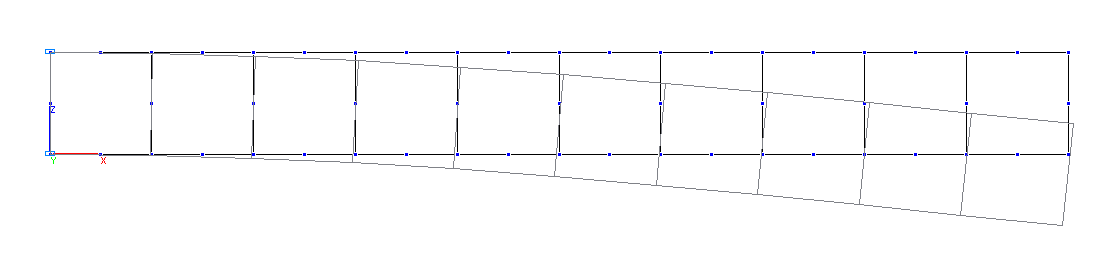
Деформированная схема. Плосконапряженная модель

Перемещения z (м). Плосконапряженная модель
Сравнение решений:
|
Модель |
Перемещения z, м |
Отклонения, % |
|---|---|---|
|
Стержневая (С) |
-1.341•10-3 |
0.00 |
|
Плосконапряженная (П) |
-1.340•10-3 |
0.07 |
|
Теория |
-1.341•10-3 |
- |
Замечания: При аналитическом решении перемещение z свободного торца балки с учетом влияния поперечного сдвига от действия сосредоточенной поперечной силы определяется по следующей формуле:
\[ z=\frac{4\cdot P\cdot L^{3}}{E\cdot t\cdot h^{3}}\cdot \left( {1+\frac{k\cdot \left( {1+\nu } \right)\cdot h^{2}}{2\cdot L^{2}}} \right). \].
