Устойчивость системы из трех одинаково нагруженных стоек разной жесткости шарнирно связанных между собой ригелями
Цель: Определение критического значения сосредоточенных продольных сил одинаковой величины, действующих на систему из трех стоек разной жесткости, шарнирно связанных между собой ригелями, соответствующего моменту потери ее устойчивости. Определение свободных длин стоек.
Файл с исходными данными: Frame_5a1.spr
Формулировка задачи: Три стойки разной жесткости, заделанные в фундамент и шарнирно объединенные между собой в систему ригелями, подвергаются воздействию сосредоточенных продольных сил одинаковой величины N. Продольные жесткости ригелей и стоек принимаются значительной величины с целью исключения их влияния на решение задачи. Определить критическое значение сосредоточенных продольных сил Ncr, соответствующее моменту потери устойчивости системы. Определить свободные длины стоек H0.
Ссылки: Н. П. Мельников, В. М. Вахуркин, Б. Г. Ложкин, Расчет стержневых систем на устойчивость. Справочные данные и примеры, Москва, Проектстальконструкция, Выпуск 1395, 1954, стр. 34.
Исходные данные:
| L = 5.0 м | - длина ригелей рамы; |
| H = 7.5 м | - высота стоек рамы; |
| EA = 1.0·109 кН | - продольная жесткость стоек; |
| EIС1 = 1.14·104 кН∙м2 | - изгибная жесткость левой стойки; |
| EIС2 = 2.28·105 кН∙м2 | - изгибная жесткость средней стойки; |
| EIС3 = 4.56·105 кН∙м2 | - изгибная жесткость правой стойки; |
| N = 1.0·103 кН | - начальное значение сосредоточенных продольных сил на стойки системы. |
Конечноэлементная модель: Расчетная схема – плоская рама, стойки – 45 элементов типа 2 (сетка конечных элементов разбита по длинам продольных осей с шагом 0.5 м), ригели – 2 элемента типа 100 (трехузловые твердые тела со связями по направлениям X и Z, ведущими узлами на середине пролетов ригелей и ведомыми узлами на сопряженных стойках). Обеспечение граничных условий достигается за счет наложения связей на опорные узлы стоек по направлениям степеней свободы X, Z, UY. Воздействие с начальным значением сосредоточенных продольных сил N задается на узлах сопряжения элементов ригелей с элементами стоек. Количество узлов в расчетной схеме – 50.
Результаты решения в SCAD
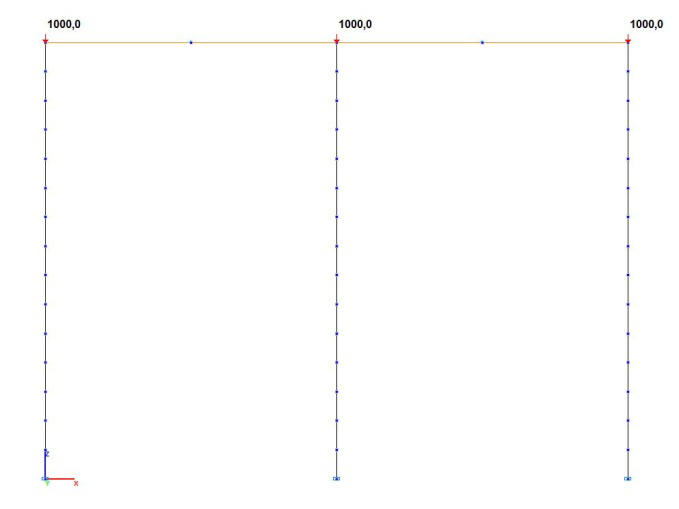
Расчетная схема

Форма потери устойчивости
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|
|
Критическое значение сосредоточенных продольных сил Ncr, кН |
1159.2 (1166.8) |
1.1591•1000 = = 1159.1 |
0.01 (0.66) |
|
Свободная длина левой стойки (С1) H0, м |
9.8522 (9.8198) |
9.8523 |
0.00 (0.33) |
|
Свободная длина средней стойки (С2) H0, м |
13.9331 (13.8873) |
13.9332 |
0.00 (0.33) |
|
Свободная длина правой стойки (С3) H0, м |
19.7043 (19.6396) |
19.7042 |
0.00 (0.33) |
В скобках приведены значения приближенного решения по методу эквивалентных рам
Замечания: При точном аналитическом решении критическое значение сосредоточенных продольных сил Ncr, соответствующее моменту потери устойчивости системы, и свободные длины стоек H0 определяются по следующим формулам:
\[ N_{cr} =\nu^{2}\cdot \frac{EI_{С1} }{H^{2}}, \]
где ν (параметр критической нагрузки) определяется из решения трансцендентного уравнения:
\[ {\begin{array}{*{20}c} {\left( {tg\left( \nu \right)-\nu } \right)\cdot \left( {tg\left( {\frac{\sqrt 2 }{2}\cdot \nu } \right)-\frac{\sqrt 2 }{2}\cdot \nu } \right)+\sqrt 2 \cdot \left( {tg\left( \nu \right)-\nu } \right)\cdot \left( {tg\left( {\frac{1}{2}\cdot \nu } \right)-\frac{1}{2}\cdot \nu } \right)+} \\ {2\cdot \left( {tg\left( {\frac{\sqrt 2 }{2}\cdot \nu } \right)-\frac{\sqrt 2 }{2}\cdot \nu } \right)\cdot \left( {tg\left( {\frac{1}{2}\cdot \nu } \right)-\frac{1}{2}\cdot \nu } \right)=0;} \\ \end{array} } \] \[ {\begin{array}{*{20}c} {С1:} & {H_{0} =\frac{\pi \cdot H}{\nu };} & {С2:} & {H_{0} =\sqrt {2\cdot } \frac{\pi \cdot H}{\nu };} & {С3:} & {H_{0} =2\cdot \frac{\pi \cdot H}{\nu }.} \\ \end{array} } \]
При приближенном аналитическом решении критическое значение сосредоточенных продольных сил Ncr, соответствующее моменту потери устойчивости системы, и свободные длины стоек H0 определяются по следующим формулам:
\[ N_{cr} =\frac{7}{3}\cdot \frac{\pi^{2}\cdot EI_{С1} }{\left( {2\cdot H} \right)^{2}}; \] \[ {\begin{array}{*{20}c} {С1:} & {H_{0} =\pi \cdot \sqrt {\frac{EI_{С1} }{N_{cr} }} ;} & {С2:} & {H_{0} =\sqrt {2\cdot } \sqrt {\frac{EI_{С1} }{N_{cr} }} ;} & {С3:} & {H_{0} =2\cdot \sqrt {\frac{EI_{С1} }{N_{cr} }} .} \\ \end{array} } \]
