Устойчивость системы из трех различно нагруженных стоек одинаковой жесткости, шарнирно связанных между собой ригелями
Цель: Определение критических значений сосредоточенных продольных сил различной величины, соответствующих моменту потери устойчивости системы в конструкции из трех стоек одинаковой жесткости, шарнирно связанных между собой ригелями. Определение свободных длин стоек.
Файл с исходными данными: Frame_5a2.spr
Формулировка задачи: Три стойки одинаковой жесткости, заделанные в фундамент и шарнирно объединенные между собой в систему ригелями, подвергаются воздействию сосредоточенных продольных сил различной величины k∙N. Продольные жесткости ригелей и стоек принимаются значительной величины с целью исключения их влияния на решение задачи. Определить критические значения сосредоточенных продольных сил Ncr, соответствующих моменту потери устойчивости системы. Определить свободные длины стоек H0.
Ссылки: Н.П. Мельников, В.М. Вахуркин, Б.Г. Ложкин, Расчет стержневых систем на устойчивость. Справочные данные и примеры, Москва, Проектстальконструкция, Выпуск 1395, 1954, стр. 36.
Исходные данные:
| L = 5.0 м | - длина ригелей рамы; |
| H = 7.5 м | - высота стоек рамы; |
| EA = 1.0·109 кН | - продольная жесткость стоек; |
| EIС = 2.28·105 кН∙м2 | - изгибная жесткость стоек; |
| 1∙N = 0.5·103 кН | - начальное значение сосредоточенной продольной силы на левой стойке; |
| 2∙N = 1.0·103 кН | - начальное значение сосредоточенной продольной силы на средней стойке; |
| 4∙N = 2.0·103 кН | - начальное значение сосредоточенной продольной силы на правой стойке. |
Конечноэлементная модель: Расчетная схема – плоская рама, стойки – 45 элементов типа 2 (сетка конечных элементов разбита по длинам продольных осей с шагом 0.5 м), ригели – 2 элемента типа 100 (трехузловые твердые тела со связями по направлениям X и Z, ведущими узлами на середине пролетов ригелей и ведомыми узлами на сопряженных стойках). Обеспечение граничных условий достигается за счет наложения связей на опорные узлы стоек по направлениям степеней свободы X, Z, UY. Воздействие с начальными значениями сосредоточенных продольных сил k•N задается на узлах сопряжения элементов ригелей с элементами стоек. Количество узлов в расчетной схеме – 50.
Результаты решения в SCAD
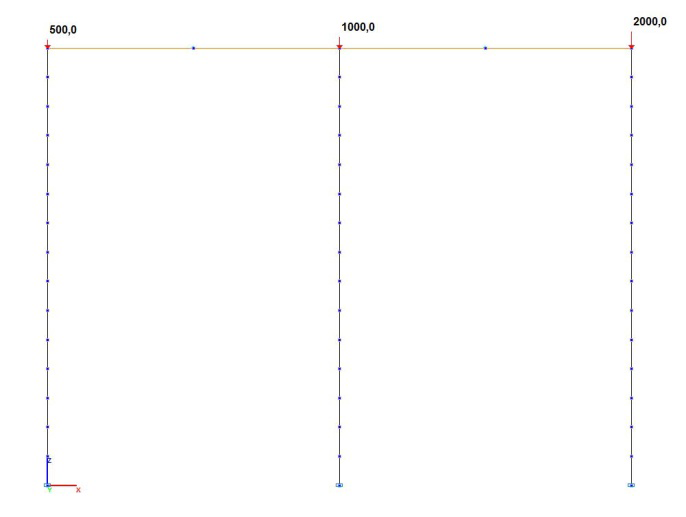
Расчетная схема
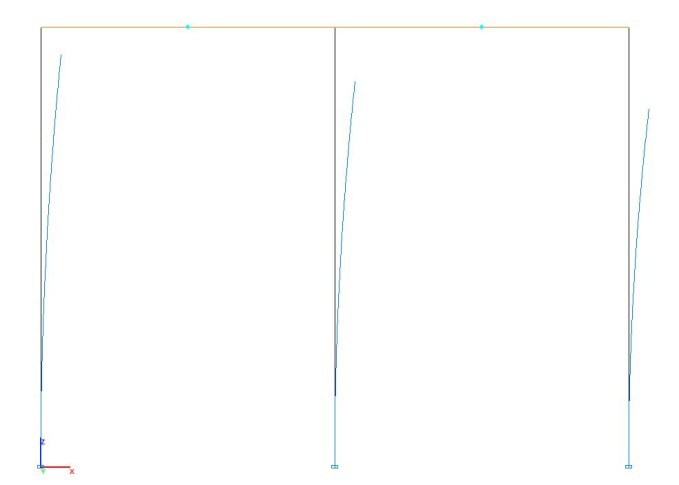
Форма потери устойчивости
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|
|
Критическое значение сосредоточенной продольной силы на левой стойке (С1) Ncr, кН |
426.6 (428.6) |
0.853157•500 = = 426.6 |
0.00 (0.47) |
|
Критическое значение сосредоточенной продольной силы на средней стойке (С2) Ncr, кН |
853.2 (857.2) |
0.853157•1000 = = 853.2 |
0.00 (0.47) |
|
Критическое значение сосредоточенной продольной силы на правой стойке (С3) Ncr, кН |
1706.3 (1714.5) |
0.853157•2000 = = 1706.3 |
0.00 (0.48) |
|
Свободная длина левой стойки (С1) H0, м |
22.9676 (22.9129) |
22.9677 |
0.00 (0.24) |
|
Свободная длина средней стойки (С2) H0, м |
16.2405 (16.2019) |
16.2406 |
0.00 (0.24) |
|
Свободная длина правой стойки (С3) H0, м |
11.4838 (11.4564) |
11.4839 |
0.00 (0.24) |
В скобках приведены значения приближенного решения по методу эквивалентных рам
Замечания: При точном аналитическом решении критические значения сосредоточенных продольных сил Ncr, соответствующее моменту потери устойчивости системы, и свободные длины стоек H0 определяются по следующим формулам:
\[ {\begin{array}{*{20}c} {С1:} & {N_{cr} =\nu^{2}\cdot \frac{EI_{С} }{H^{2}}} & {С2:} & {N_{cr} =2\cdot \nu^{2}\cdot \frac{EI_{С} }{H^{2}}} & {С3:} & {4\cdot \nu^{2}\cdot \frac{EI_{С} }{H^{2}}} \\ \end{array} }, \]
где ν (параметр критической нагрузки) определяется из решения трансцендентного уравнения:
\[ {\begin{array}{*{20}c} {\left( {tg\left( \nu \right)-\nu } \right)\cdot \left( {tg\left( {\sqrt 2 \cdot \nu } \right)-\sqrt 2 \cdot \nu } \right)+\frac{\sqrt 2 }{4}\cdot \left( {tg\left( \nu \right)-\nu } \right)\cdot \left( {tg\left( {2\cdot \nu } \right)-2\cdot \nu } \right)+} \\ {+\frac{1}{8}\cdot \left( {tg\left( {\sqrt 2 \cdot \nu } \right)-\sqrt 2 \cdot \nu } \right)\cdot \left( {tg\left( {2\cdot \nu } \right)-2\cdot \nu } \right)=0;} \\ \end{array} } \] \[ {\begin{array}{*{20}c} {С1:} & {H_{0} =\frac{\pi \cdot H}{\nu };} & {С2:} & {H_{0} =\frac{\sqrt 2 }{2}\frac{\pi \cdot H}{\nu };} & {С3:} & {H_{0} =\frac{1}{2}\cdot \frac{\pi \cdot H}{\nu }.} \\ \end{array} } \]
При приближенном аналитическом решении критическое значение сосредоточенных продольных сил Ncr, соответствующее моменту потери устойчивости системы, и свободные длины стоек H0 определяются по следующим формулам:
\[ {\begin{array}{*{20}c} {С1:} & {N_{cr} =\frac{3}{7}\cdot \frac{\pi^{2}\cdot EI_{С} }{\left( {2\cdot H} \right)^{2}}} & {С2:} & {N_{cr} =\frac{6}{7}\cdot \frac{\pi^{2}\cdot EI_{С} }{\left( {2\cdot H} \right)^{2}}} & {С3:} & {N_{cr} =\frac{12}{7}\cdot \frac{\pi ^{2}\cdot EI_{С} }{\left( {2\cdot H} \right)^{2}}} \\ \end{array} }; \] \[ H_{0} =\pi \cdot \sqrt {\frac{EI_{С} }{N_{cr} }} . \]
