Устойчивость трехпролетной двухэтажной рамы под действием сосредоточенных продольных сил на стойки в узлах сопряжения с ригелями
Цель: Определение критического значения сосредоточенных продольных сил, действующих на стойки трехпролетной двухэтажной рамы в узлах сопряжения с ригелями, соответствующего моменту потери ее устойчивости.
Файл с исходными данными: 6.1.spr
Формулировка задачи: Трехпролетная двухэтажная рама подвергается воздействию сосредоточенных продольных сил P на стойки в узлах сопряжения с ригелями. Узлы сопряжения ригелей со стойками и узлы опирания на фундамент являются жесткими. Продольные жесткости ригелей и стоек принимаются значительной величины с целью исключения их влияния на решение задачи. Определить критическое значение сосредоточенных продольных сил Pcr, соответствующее моменту потери устойчивости рамы.
Ссылки: Н. В. Корноухов, Прочность и устойчивость стержневых систем, Москва, Стройиздат, 1949, стр. 259.
Исходные данные:
| L = 8.0 м | - длина ригелей рамы; |
| H = 4.0 м | - высота стоек рамы; |
| EA = 1.0·1010 кН | - продольная жесткость конструктивных элементов рамы; |
| EIС1 = 8.00·105 кН∙м2 | - изгибная жесткость стоек первого этажа; |
| iС1 = EIС1/H = 2.0·105 кН∙м | - погонная изгибная жесткость стоек первого этажа; |
| EIС2 = 4.00·105 кН∙м2 | - изгибная жесткость стоек второго этажа; |
| iС2 = EIС2/H = 1.00·105 кН∙м | - погонная изгибная жесткость стоек второго этажа; |
| EIР1 = 13.28·105 кН∙м2 | - изгибная жесткость ригелей первого этажа; |
| iР1 = EIР1/L = 1.66·105 кН∙м | - погонная изгибная жесткость ригелей первого этажа; |
| EIР2 = 8.00·105 кН∙м2 | - изгибная жесткость ригелей второго этажа; |
| iР2 = EIР2/L = 1.00·105 кН∙м | - погонная изгибная жесткость ригелей второго этажа; |
| P = 1.0·105 кН | - начальное значение сосредоточенных продольных сил на стойки рамы в узлах сопряжения с ригелями. |
Конечноэлементная модель: Расчетная схема – плоская рама, 80 элементов типа 2. Сетка конечных элементов разбита по длинам продольных осей конструктивных элементов (вдоль осей X1 местных систем координат) с шагом 1.0 м. Обеспечение граничных условий достигается за счет наложения связей на опорные узлы рамы по направлениям степеней свободы X, Z, UY. Воздействие с начальным значением сосредоточенных продольных сил P задается на узлах сопряжения элементов ригелей с элементами стоек. Количество узлов в расчетной схеме – 78.
Результаты решения в SCAD
Расчетная схема
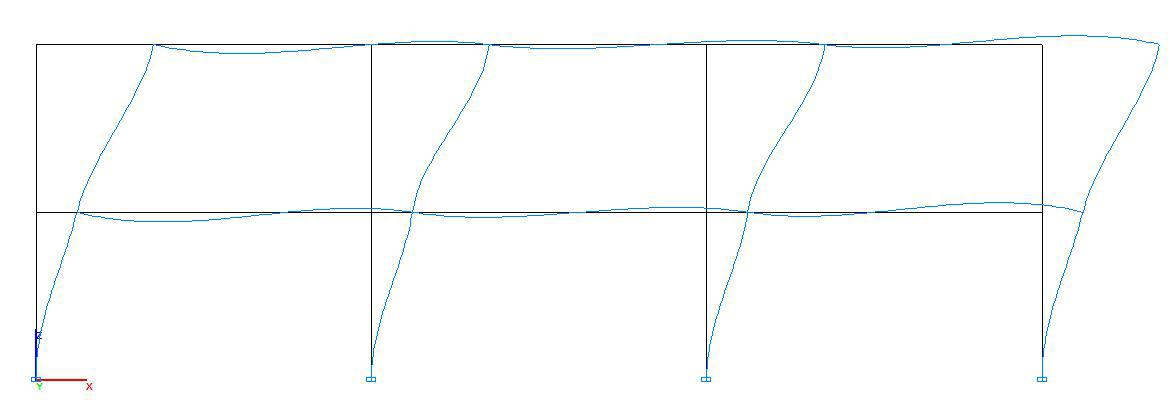
Форма потери устойчивости
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|
|
Критическое значение сосредоточенных продольных сил Pcr, кН |
156250 |
1.5625•100000 = = 156250 |
0.00 |
Замечания: При аналитическом решении критическое значение сосредоточенных продольных сил Pcr, соответствующее моменту потери устойчивости рамы, определяется по следующей формуле:
\[ P_{cr} =2.5000^{2}\cdot \frac{i_{С1} }{H}. \]
