Устойчивость круговой двухшарнирной арки постоянного сечения при гидростатическом давлении
Цель: Определение критического значения гидростатического давления, действующего на свод круговой двухшарнирной арки постоянного сечения, соответствующего моменту потери ее устойчивости.
Формулировка задачи: Круговая двухшарнирная арка постоянного сечения подвергается воздействию равномерно распределенной радиальной нагрузки q. Определить критическое значение равномерно распределенной радиальной нагрузки qcr, соответствующее моменту потери устойчивости арки. Принять, что при потере устойчивости элементы нагрузки следуют за осью арки, сохраняя параллельность своим прежним направлениям, благодаря чему происходит перемещение линии давления при потере устойчивости арки. Сравнить результат расчета с решением (С. П. Тимошенко), когда элементы нагрузки при искривлении оси арки сохраняют линии своего действия и линия давления при потере устойчивости арки не перемещается.
Ссылки: Н. В. Корноухов, Прочность и устойчивость стержневых систем, Москва, Стройиздат, 1949, стр. 212.
Исходные данные:
| R = 60.0 м (120.0 м) | - радиус продольной оси арки; |
| 2∙ω = 2∙90 ° (2∙30 °) | - центральный угол дуги арки; |
| EA = 2.16·106 кН | - продольная жесткость арки; |
| EI = 2.592·105 кН∙м2 | - изгибная жесткость арки; |
| q = 1.0 кН/м | - начальное значение равномерно распределенной радиальной нагрузки на арку. |
Файлы с исходными данными:
| Arch_hinged_alfa_30.spr | Расчетная схема с центральным углом дуги арки 2∙ω = 2∙30 ° |
| Arch_hinged_alfa_90.spr | Расчетная схема с центральным углом дуги арки 2∙ω = 2∙90 ° |
Конечноэлементная модель: Расчетная схема – плоская рама, 36 элементов типа 2. Сетка конечных элементов разбита по длине продольной оси арки (вдоль осей X1 местных систем координат) с шагом центрального угла 5.0 ° (1.667 °). Обеспечение граничных условий достигается за счет наложения связей на опорные узлы арки по направлениям степеней свободы X, Z. Воздействие с начальным значением равномерно распределенной радиальной нагрузки q задается по направлениям против осей Z1 местных систем координат элементов. Количество узлов в расчетной схеме – 37.
Результаты решения в SCAD
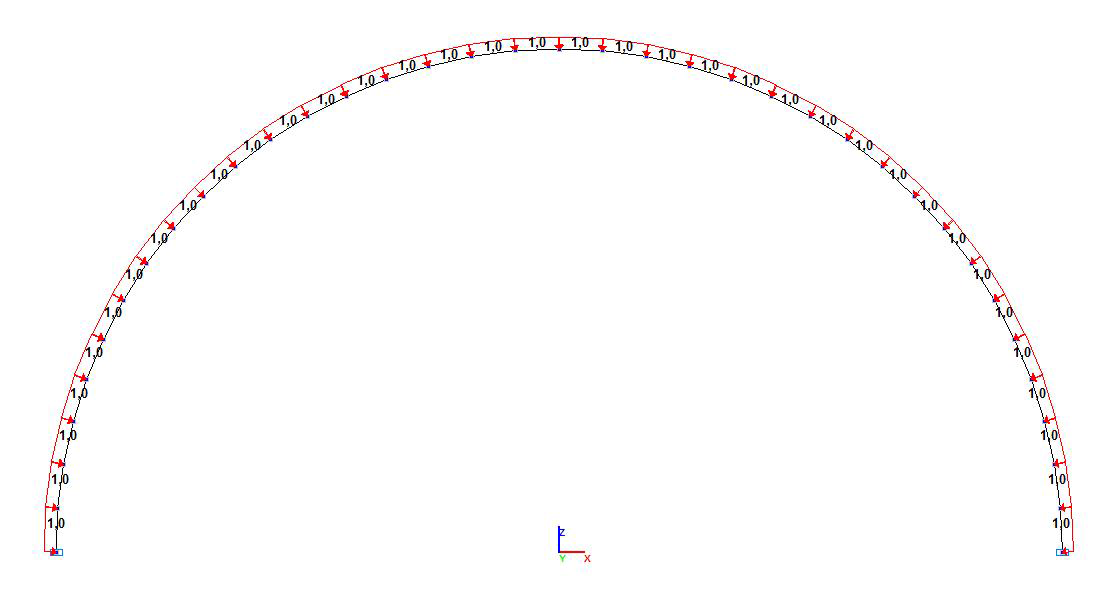
Расчетная схема с центральным углом дуги арки 2•90 °
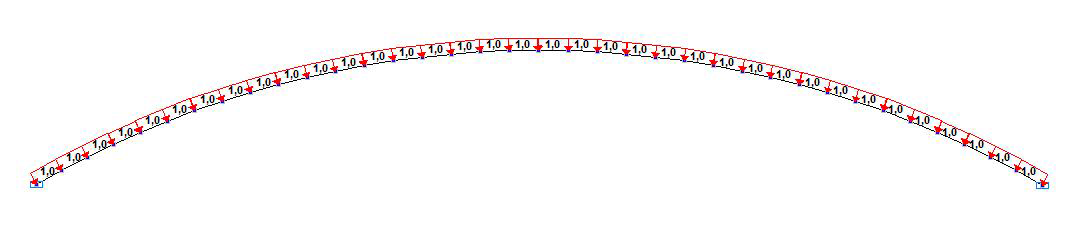
Расчетная схема с центральным углом дуги арки 2•30 °
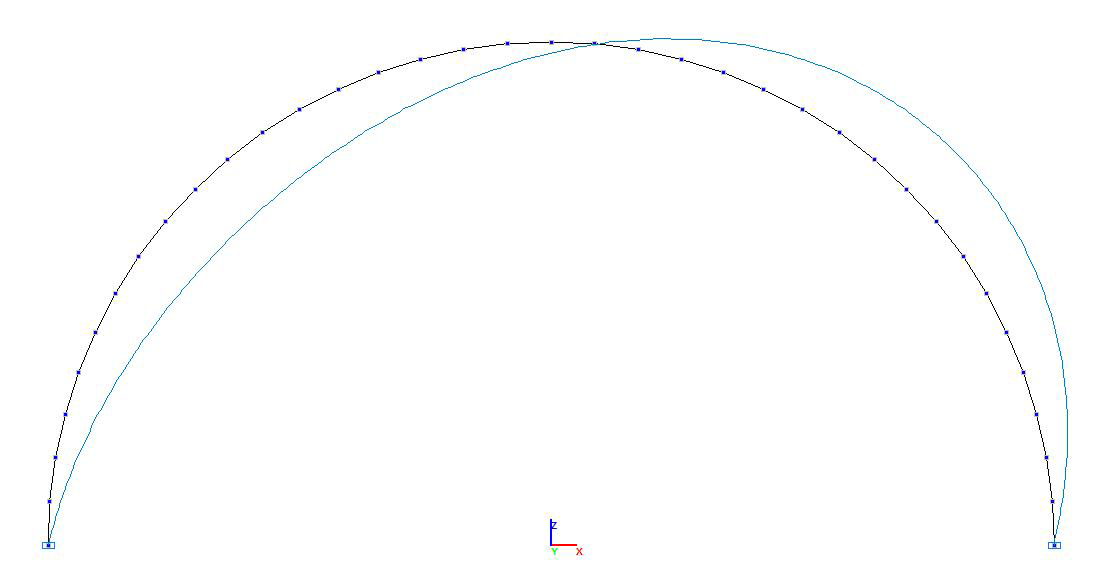
Форма потери устойчивости для схемы с центральным углом дуги арки 2•90 °
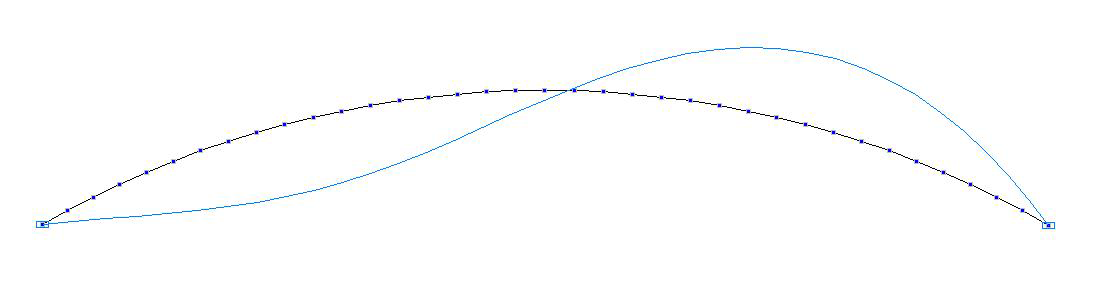
Форма потери устойчивости для схемы с центральным углом дуги арки 2•30 °
Сравнение решений:
Критическое значение равномерно распределенной радиальной нагрузки на арку qcr, кН/м
|
Расчетная схема |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|
|
с центральным углом дуги арки 2•90 ° |
3.925 (3.600) [3.932] |
3.933914•1.0 = = 3.934 |
0.23 (9.28) [0.05] |
|
с центральным углом дуги арки 2•30 ° |
5.391 (5.250) [5.392] |
5.393093•1.0 = = 5.393 |
0.04 (2.72) [0.02] |
Без скобок указаны теоретические значения, посчитанные по условиям данного примера (по Н. В. Корноухову);
В круглых скобках указаны теоретические значения, посчитанные по условиям решения С. П. Тимошенко;
В квадратных скобках указаны теоретические значения, посчитанные для двухшарнирной рамы, составленной из 2∙m=36 равных хорд, вписанных в дугу окружности, и подверженной действию равных радиальных сил во всех ее узлах.
Замечания: При аналитическом решении по условиям Н. В. Корноухова критическое значение равномерно распределенной радиальной нагрузки qcr, соответствующее моменту потери устойчивости арки определяется по следующей формуле:
\[ q_{cr} =\eta^{2}\cdot \frac{EI}{R^{3}}, \]
где η (параметр критической нагрузки) определяется из решения трансцендентного уравнения:
\[ \frac{1}{\left( {\eta^{2}-1} \right)^{2}}\cdot \left[ {\eta^{3}\cdot \left( {\omega +\frac{1}{2}\cdot \sin \left( {2\cdot \omega } \right)} \right)-\eta \cdot \left( {\omega +\frac{3}{2}\cdot \sin \left( {2\cdot \omega } \right)} \right)+\frac{1-\cos \left( {2\cdot \omega } \right)}{tg\left( {\eta \cdot \omega } \right)}} \right]=0. \]
При аналитическом решении по условиям С. П. Тимошенко критическое значение равномерно распределенной радиальной нагрузки qcr, соответствующее моменту потери устойчивости арки определяется по следующей формуле:
\[ q_{cr} =\frac{EI}{R^{3}}\cdot \left( {\frac{\pi^{2}}{\omega^{2}}-1} \right). \]
При аналитическом решении для двухшарнирной рамы, составленной из равных хорд, вписанных в дугу окружности, критическое значение равномерно распределенной радиальной нагрузки qcr, соответствующее моменту потери ее устойчивости определяется по следующей формуле:
\[ q_{cr} =2\cdot \upsilon^{2}\cdot \frac{EI}{L^{3}}\cdot \sin \left( {\frac{A}{2}} \right), \]
где υ (параметр критической нагрузки) определяется из решения трансцендентного уравнения:
\[ \left( {1-\frac{\sin \left( \upsilon \right)}{\upsilon }\cdot \frac{1-\cos \left( A \right)}{\cos \left( \upsilon \right)-\cos \left( A \right)}} \right)\cdot \left( {m+\frac{\sin \left( {2\cdot m\cdot A} \right)}{2\cdot \sin \left( A \right)}} \right)+\left( {\frac{2\cdot \sin \left( {\frac{A}{2}} \right)\cdot \sin \left( {\frac{\upsilon }{2}} \right)}{\cos \left( \upsilon \right)-\cos \left( A \right)}\cdot \frac{\sin \left( \upsilon \right)}{\upsilon }\cdot \frac{\sin \left( {m\cdot A} \right)}{\sin \left( {m\cdot \upsilon } \right)}} \right)\cdot \left( {\frac{\sin \left( {m\cdot \left( {A+\upsilon } \right)} \right)}{2\cdot \sin \left( {\frac{A+\upsilon }{2}} \right)}+\frac{\sin \left( {m\cdot \left( {A-\upsilon } \right)} \right)}{2\cdot \sin \left( {\frac{A-\upsilon }{2}} \right)}} \right)=0. \]
2∙m - число хорд рамы,
A - центральный угол одной хорды рамы,
L - длина одной хорды рамы:
\[ L=R\cdot \sqrt {2\cdot \left( {1-\cos \left( A \right)} \right)} . \]
