Устойчивость квадратной шарнирно опертой пластины равномерно сжатой в одном направлении

Цель: Определение критического значения сжимающих усилий, равномерно распределенных по двум противоположным сторонам квадратной шарнирно опертой пластины, соответствующего моменту потери ее устойчивости.

Файлы с исходными данными:

6.7_n_4.spr	Расчетная модель с четырехузловыми элементами оболочки типа 44
6.7_n_8.spr	Расчетная модель с восьмиузловыми элементами оболочки типа 50

Формулировка задачи: Квадратная пластина подвергается воздействию сжимающих усилий σ, равномерно распределенных по двум противоположным сторонам, имеющим шарнирно-подвижное (свободное) опирание. Две другие противоположные стороны пластины, свободные от воздействий, имеют шарнирно-неподвижное опирание. Определить критическое значение сжимающих усилий σ_cr, соответствующее моменту потери устойчивости квадратной пластины. 

Ссылки: J.H. Argyris, P.C. Dunne, G.A. Malejannakis, E. Schelkle. A simple triangular facet shell element with applications to linear and non-linear equilibrium and elastic stability problems. Computer methods in applied mechanics and engineering, 11. — 1977.— p. 97-131.
S.P. Timoshenko, J.M. Gere. Theory of elastic stability. McGraw-Hill. — New York. — 1963. — p. 356.

Исходные данные:

a = 8.0 м	- размер стороны квадратной пластины;
h = 0.08 м	- толщина квадратной пластины;
E = 1.0·107 кН/м2	- модуль упругости материала квадратной пластины;
ν = 1/3	- коэффициент Пуассона;
σ = 1.25·103 кН/м2	- начальное значение сжимающих усилий.

Конечноэлементная модель: Расчетная  схема – система общего вида. Рассматриваются две расчетные модели с четырехузловыми элементами оболочки типа 44 и с восьмиузловыми элементами оболочки типа 50. Сетка конечных элементов разбита по сторонам пластины (вдоль осей X и Y общей системы координат) с шагом 1.0 м.  Количество элементов в схеме – 64. Обеспечение граничных условий достигается за счет наложения связей на узлы опорного контура пластины по направлению степени свободы Z, а также за счет наложения связей на узлы двух противоположных сторон пластины, свободных от воздействий по нормальному к ним направлению вдоль оси Y общей системы координат. На одной из двух противоположных сторон пластины, подверженных воздействию сжимающих усилий, задается равномерно распределенная по линии нагрузка с начальным значением p = σ∙h = 100 кН/м, а на узлы другой накладываются связи по соответствующему направлению (вдоль оси X общей системы координат). В целях обеспечения геометрической неизменяемости расчетной схемы на один узел контура опирания пластины накладывается связь по направлению UZ общей системы координат. Количество узлов по моделям – 81; 225.

Результаты решения в SCAD

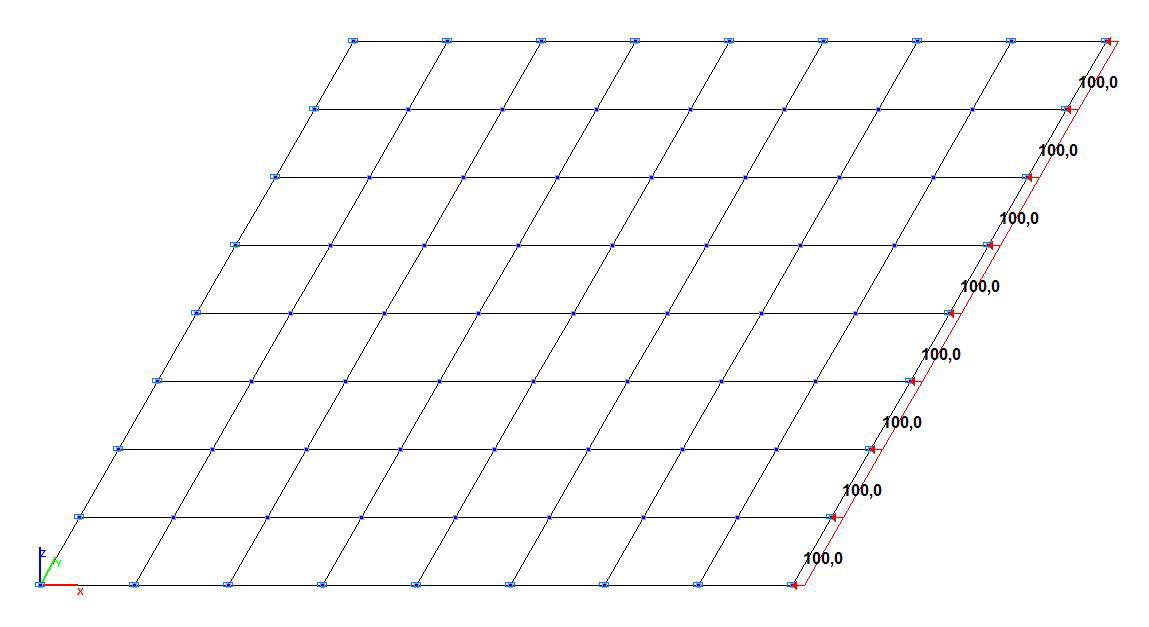
Расчетная схема. Модель с четырехузловыми элементами оболочки

 

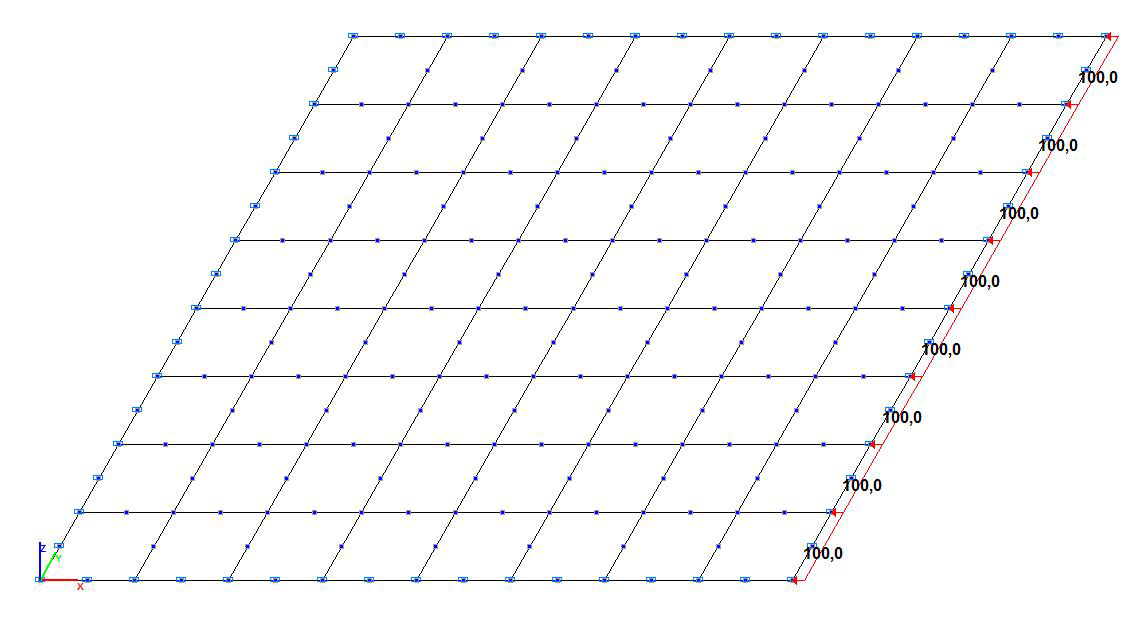
Расчетная схема. Модель с восьмиузловыми элементами оболочки

 

 
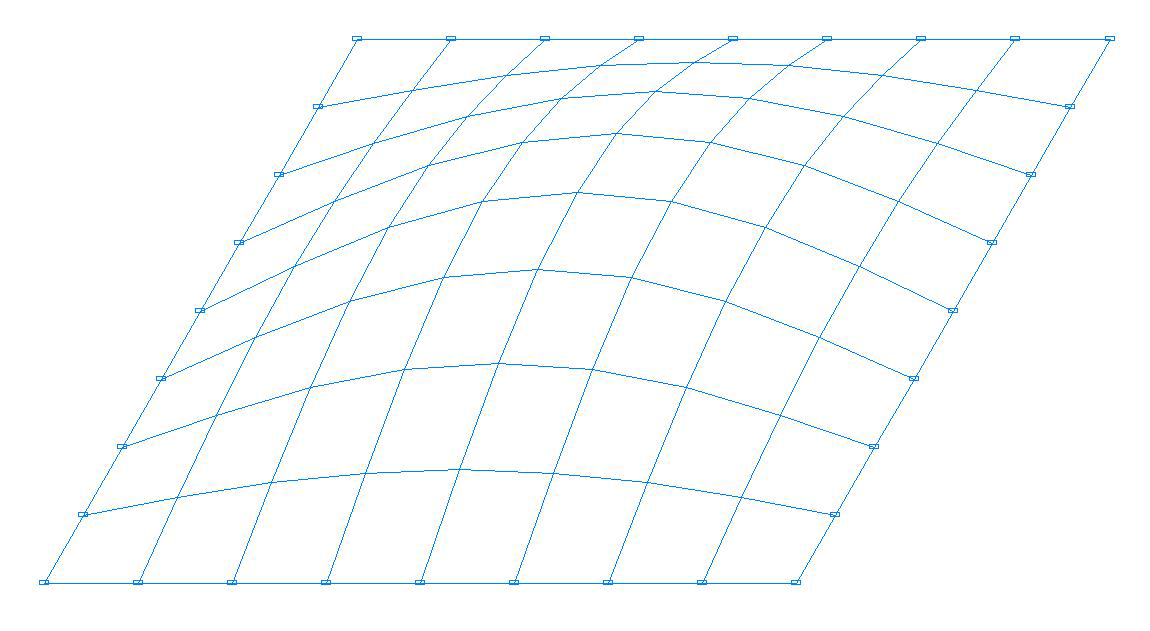
Форма потери устойчивости. Модель с четырехузловыми элементами оболочки

 

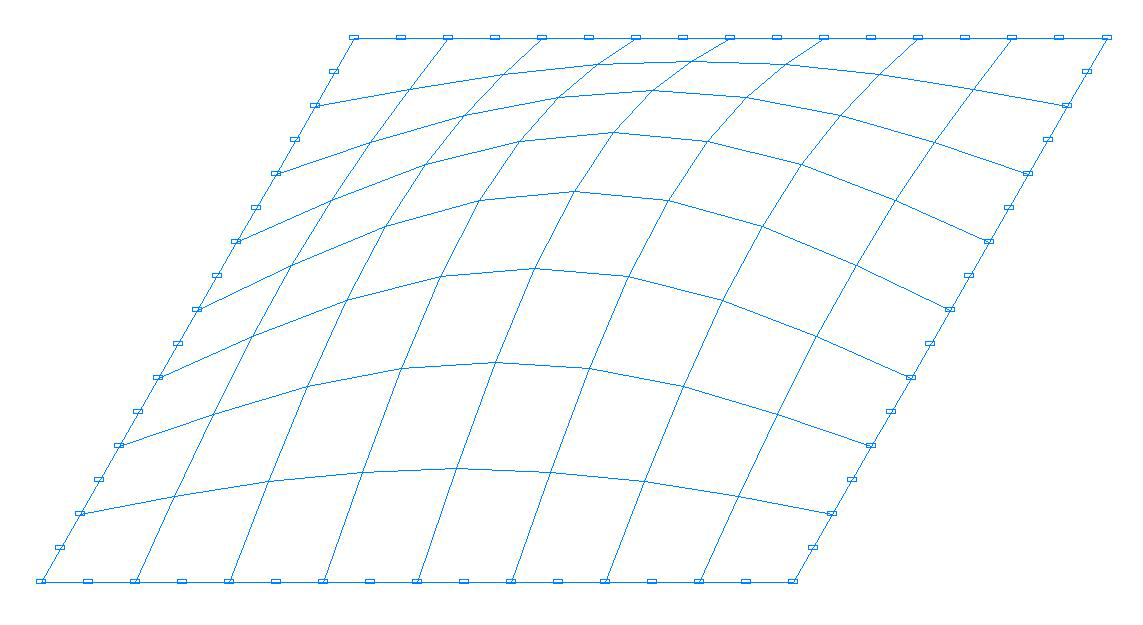
Форма потери устойчивости. Модель с восьмиузловыми элементами оболочки

 

Сравнение решений:

Критическое значение сжимающих усилий σ_cr, кН/м²

Расчетная модель	Теория	SCAD	Отклонение, %
Тип элемента 44 n = 4 узла	2776	2.248923∙100/0.08 = = 2811	1.26
Тип элемента 50 n = 8 узлов		2.220676∙100/0.08 = = 2776	0.00

Замечания: При аналитическом решении критическое значение сжимающих усилий σ_cr, соответствующее моменту потери устойчивости квадратной пластины определяется по следующей формуле:

\[ \sigma_{cr} =\frac{4\cdot \pi^{2}\cdot D}{\left( {1+\nu } \right)\cdot a^{2}\cdot h}, \quad где: \quad D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}. \]