Устойчивость прямоугольной свободно опертой пластины при чистом сдвиге
Цель: Определение критического значения сдвигающих усилий, равномерно распределенных по противоположным сторонам прямоугольной свободно опертой пластины, соответствующего моменту потери ее устойчивости.
Файлы с исходными данными:
| 6.9_a_8_n_4.spr | Расчетная схема с соотношениями сторон пластины a/b = 1.0 с моделью из четырехузловых элементов оболочки типа 44 |
| 6.9_a_8_n_8.spr | Расчетная схема с соотношениями сторон пластины a/b = 1.0 с моделью из восьмиузловых элементов оболочки типа 50 |
| 6.9_a_16_n_4.spr | Расчетная схема с соотношениями сторон пластины a/b = 2.0 с моделью из четырехузловых элементов оболочки типа 44 |
| 6.9_a_16_n_8.spr | Расчетная схема с соотношениями сторон пластины a/b = 2.0 с моделью из восьмиузловых элементов оболочки типа 50 |
Формулировка задачи: Прямоугольная свободно опертая пластина подвергается воздействию сдвигающих усилий τ, равномерно распределенных по противоположным сторонам. Определить критическое значение сжимающих усилий τcr, соответствующее моменту потери устойчивости прямоугольной пластины.
Ссылки: С. П. Тимошенко, Устойчивость стержней, пластин и оболочек, Москва, Наука, 1971, стр. 626.
А. С. Вольмир, Устойчивость деформируемых систем, Москва, Наука, 1967, стр. 344.
Исходные данные:
| a = 8.0; 16.0 м | - размер стороны прямоугольной пластины вдоль оси X общей системы координат; |
| b = 8.0 м | - размер стороны прямоугольной пластины вдоль оси Y общей системы координат; |
| h = 0.08 м | - толщина прямоугольной пластины; |
| E = 1.0·107 кН/м2 | - модуль упругости материала прямоугольной пластины; |
| ν = 1/3 | - коэффициент Пуассона; |
| σ = 1.25·103 кН/м2 | - начальное значение сдвигающих усилий. |
Конечноэлементная модель: Расчетная схема – система общего вида. Для двух расчетных схем с соотношениями сторон пластины a/b = 1.0; 2.0 рассматриваются две расчетные модели с четырехузловыми элементами оболочки типа 44 и с восьмиузловыми элементами оболочки типа 50. Сетка конечных элементов разбита по сторонам пластины (вдоль осей X и Y общей системы координат) с шагом 1.0 м. Количество элементов по схемам – 64; 128. Обеспечение граничных условий достигается за счет наложения связей на узлы опорного контура пластины по направлению степени свободы Z. На одной из двух противоположных сторон пластины, расположенных вдоль оси X общей системы координат, задается равномерно распределенная по линии нагрузка с начальным значением p = -τ∙h = -100 кН/м, а на узлы другой (расположенной на оси X) накладываются связи по направлениям степеней свободы X и Y. На одной из двух противоположных сторон пластины, расположенных вдоль оси Y общей системы координат, задается равномерно распределенная по линии нагрузка с начальным значением p = -τ∙h = -100 кН/м, а на другой (расположенной на оси Y) задается равномерно распределенная по линии нагрузка с начальным значением p = τ∙h = 100 кН/м. В целях обеспечения геометрической неизменяемости расчетной схемы на узел одного из углов пластины накладывается связь по направлению UZ общей системы координат. Количество узлов по схемам (моделям) – 81 (225); 153 (433).
Результаты решения в SCAD
Расчетные модели для схем с соотношением сторон пластины a/b = 1.0
Расчетные модели для схем с соотношением сторон пластины a/b = 2.0
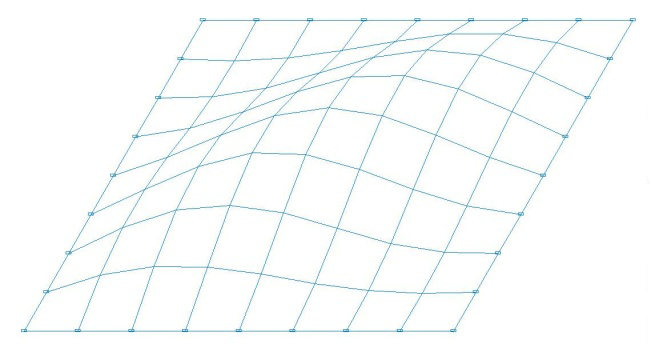
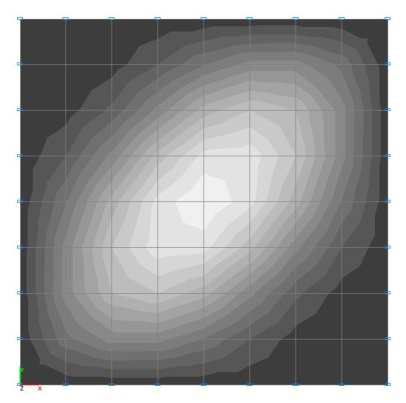
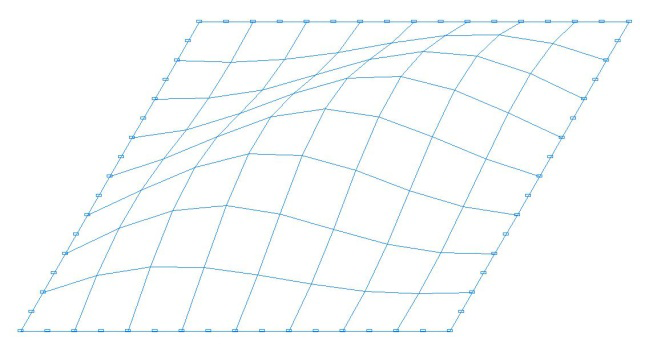

Формы потери устойчивости расчетных моделей для схем с соотношением сторон пластины a/b = 1.0
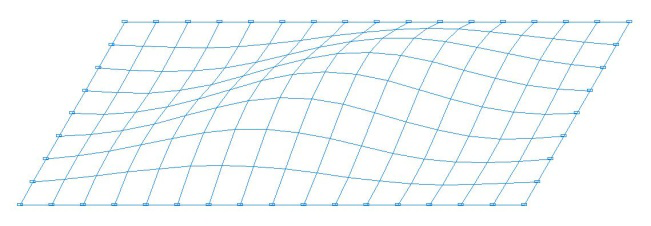
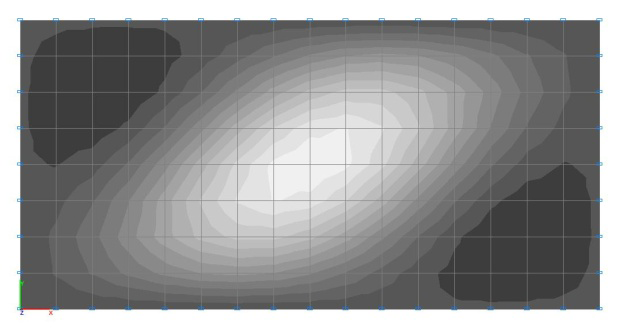
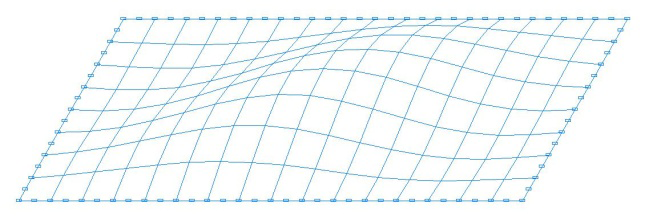

Формы потери устойчивости расчетных моделей для схем с соотношением сторон пластины a/b = 2.0
Сравнение решений:
Критическое значение сдвигающих усилий τcr, кН/м2
|
Расчетная схема |
Расчетная модель |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|---|
|
a/b = 1.0 |
Тип элемента 44 n = 4 узла |
8631 |
7.129409∙100/0.08 = = 8912 |
3.26 |
|
Тип элемента 50 n = 8 узлов |
6.903095∙100/0.08 = = 8629 |
0.02 |
||
|
a/b = 2.0 |
Тип элемента 44 n = 4 узла |
6060 |
4.930113∙100/0.08 = = 6163 |
1.70 |
|
Тип элемента 50 n = 8 узлов |
4.845765∙100/0.08 = = 6057 |
0.05 |
Замечания: При аналитическом решении критическое значение сдвигающих усилий τcr, соответствующее моменту потери устойчивости прямоугольной пластины определяется по следующей формуле:
\[ \sigma_{cr} =k\cdot \frac{\pi^{2}\cdot D}{b^{2}\cdot h}, \quad где: \quad \] \[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}, \quad k=\frac{\pi^{2}}{32\cdot \alpha^{3}\cdot \lambda }, \quad \alpha =\frac{a}{b}. \]
Параметр λ вычисляется из условия равенства нулю определителя системы уравнений:
\[ \lambda \cdot \left( {m^{2}+\alpha^{2}\cdot n^{2}} \right)\cdot A_{mn} -\sum\limits_i {\sum\limits_j {\frac{m\cdot n\cdot i\cdot j}{\left( {m^{2}-i^{2}} \right)\cdot \left( {n^{2}-j^{2}} \right)}\cdot A_{ij} =0,} } \]
в которых принимаются следующие сочетания индексов:
| m + i n + j m + n |
нечетные нечетные четные |
При m, n, i, j = 1, 2, 3, 4, 5, 6, 7, 8 (определитель имеет размерность 32∙32) имеем:
\[ {\begin{array}{*{20}c} {\frac{a}{b}=1.0} & {k=9.328} \\ {\frac{a}{b}=2.0} & {k=6.549.} \\ \end{array} } \]
