Устойчивость прямоугольной ортотропной свободно опертой пластины равномерно сжатой в одном направлении
Цель: Определение критического значения сжимающих усилий, равномерно распределенных по двум противоположным поперечным торцам прямоугольной ортотропной свободно опертой пластины, соответствующего моменту потери ее устойчивости.
Файлы с исходными данными:
| 6.10_shell_orthotropic_lambda_1.spr | Расчетная схема с соотношениями сторон пластины a/b = 1.0 |
| 6.10_shell_orthotropic_lambda_4.spr | Расчетная схема с соотношениями сторон пластины a/b = 4.0 |
Формулировка задачи: Прямоугольная ортотропная свободно опертая пластина подвергается воздействию сжимающих усилий σ, равномерно распределенных по двум противоположным поперечным торцам. Определить критическое значение сжимающих усилий σcrort, соответствующее моменту потери устойчивости прямоугольной ортотропной пластины.
Ссылки: А. С. Вольмир, Устойчивость деформируемых систем, Москва, Наука, 1967, стр. 374.
Исходные данные:
| a = 0.6; 2.4 м | - размер стороны прямоугольной пластины, свободной от воздействий (вдоль оси X общей системы координат); |
| b = 0.6 м | - размер стороны прямоугольной пластины, подверженной воздействию сжимающих усилий (вдоль оси Y общей системы координат); |
| h = 0.01 м | - толщина прямоугольной пластины; |
| Ex = 5.600·108 кН/м2 | - модуль упругости материала пластины, отвечающий продольным деформациям по оси X общей системы координат; |
| νyx = 0.300 | - коэффициент Пуассона, отвечающий поперечным деформациям по оси Y общей системы координат; |
| Ey = 2.123·108 кН/м2 | - модуль упругости материала пластины, отвечающий продольным деформациям по оси Y общей системы координат; |
| νxy = 0.114 | - коэффициент Пуассона, отвечающий поперечным деформациям по оси X общей системы координат; |
| Gxy = 0.769·108 кН/м2 | - модуль сдвига материала пластины; |
| σ = 1.0·105 кН/м2 | - начальное значение сжимающих усилий. |
Конечноэлементная модель: Расчетная схема – система общего вида. Рассматриваются две расчетные схемы с соотношениями сторон пластины a/b = 1.0; 4.0. Пластина моделируется восьмиузловыми элементами оболочки типа 50. Сетка конечных элементов разбита по сторонам пластины (вдоль осей X и Y общей системы координат) с шагом 0.075 м. Количество элементов пластины по схемам – 64; 256. Обеспечение граничных условий достигается за счет наложения связей на узлы опорного контура пластины по направлению степени свободы Z. На одном из двух противоположных поперечных торцов пластины, подверженных воздействию сжимающих усилий, задается равномерно распределенная по линии нагрузка с начальным значением p = σ•h = 1000 кН/м, а на узлы другого накладываются связи по соответствующему направлению (вдоль оси X общей системы координат). В целях обеспечения геометрической неизменяемости расчетной схемы на узлы одного из двух противоположных продольных торцов пластины, свободных от воздействий, накладываются связи по нормальному к нему направлению (вдоль оси Y общей системы координат). В этих же целях на узел одного из углов пластины накладывается связь по направлению UZ общей системы координат. Количество узлов по схемам – 225; 849.
Результаты решения в SCAD
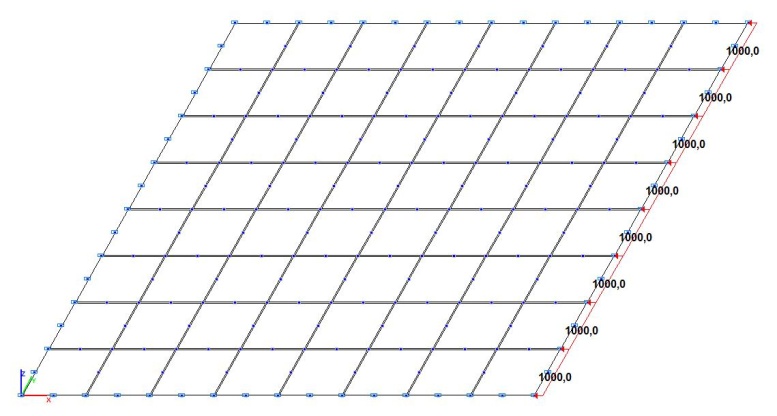
Расчетная схема с соотношением сторон пластины a/b = 1.0
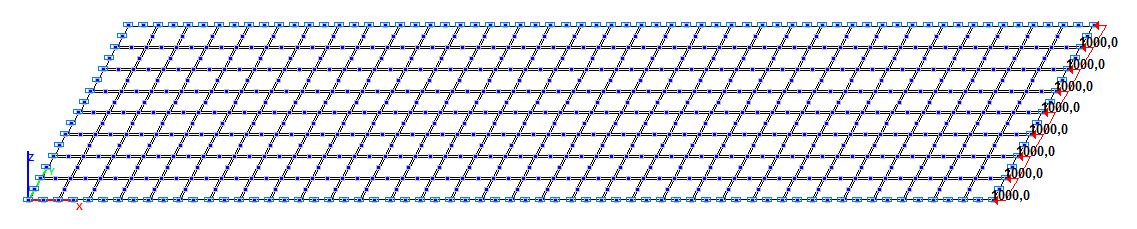
Расчетная схема с соотношением сторон пластины a/b = 4.0
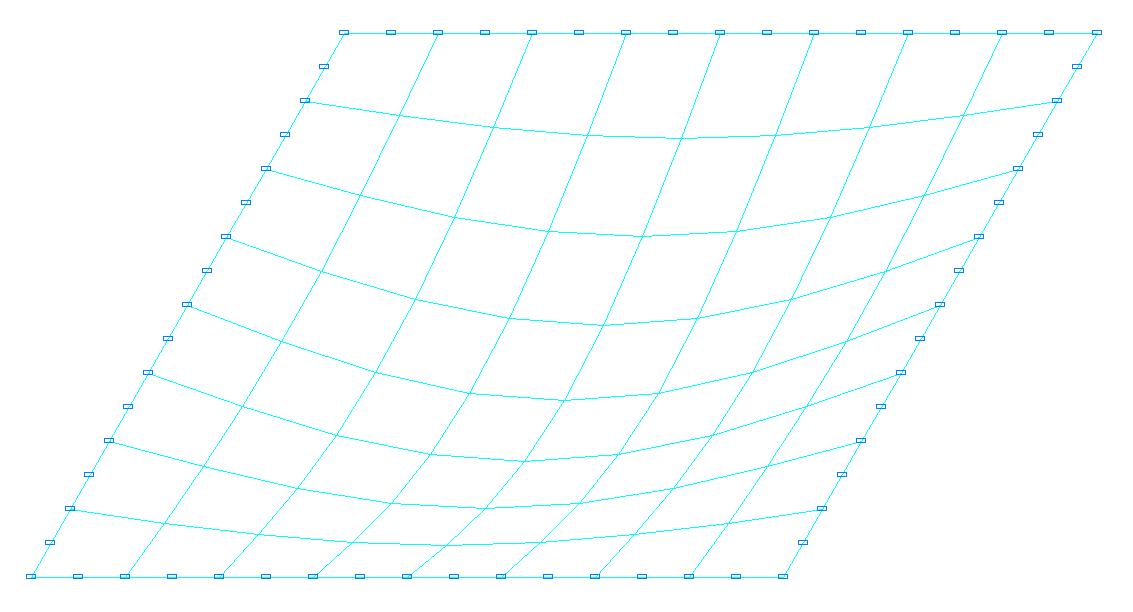
1-я форма потери устойчивости для расчетной схемы с соотношением сторон пластины a/b = 1.0
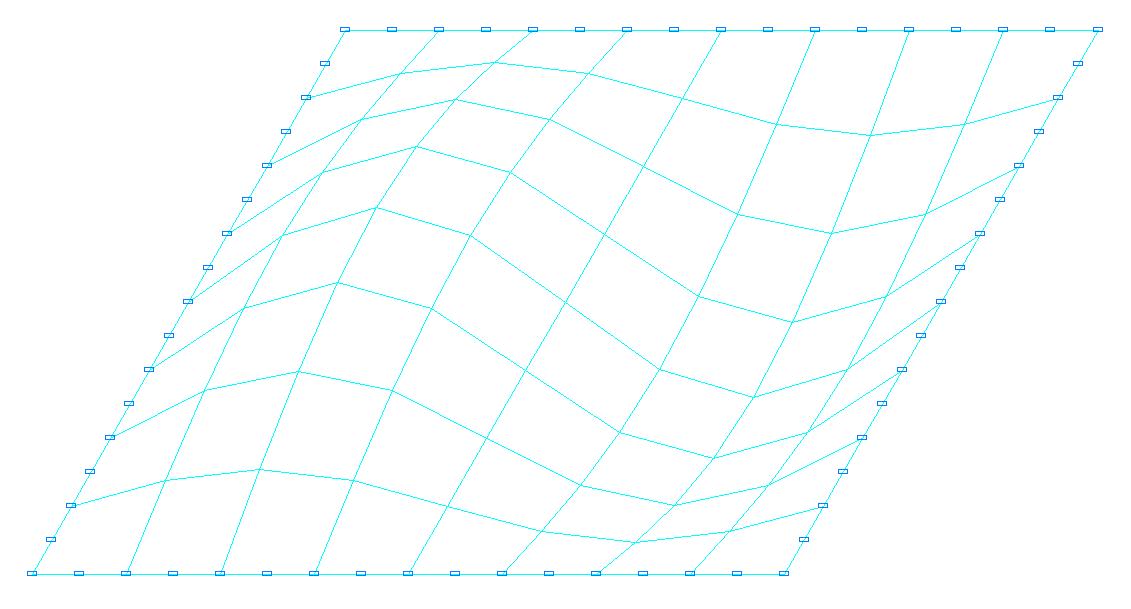
2-я форма потери устойчивости для расчетной схемы с соотношением сторон пластины a/b = 1.0
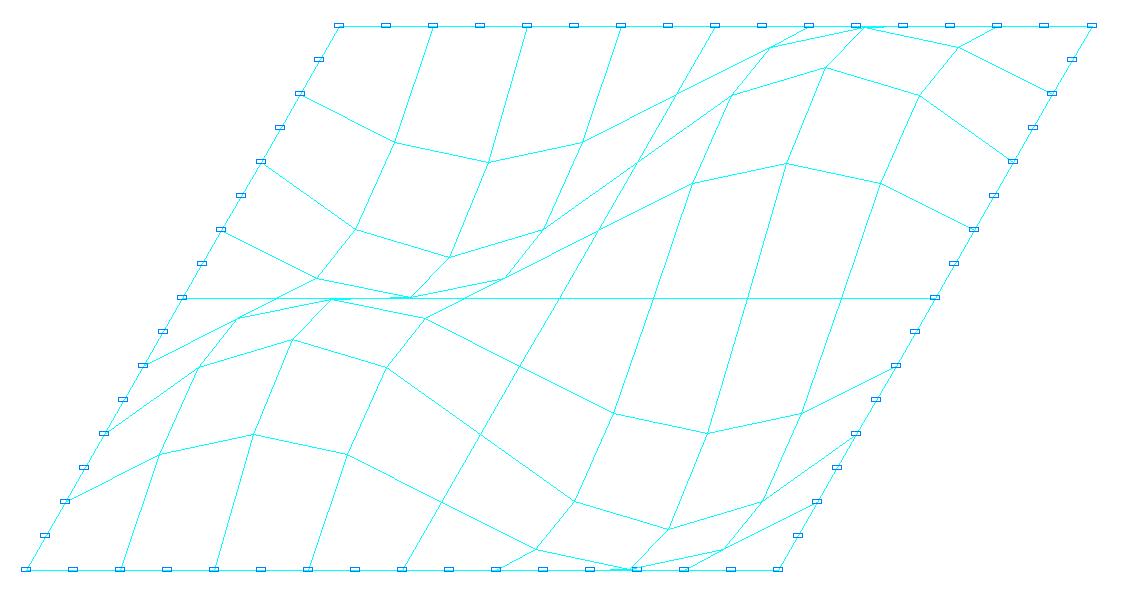
3-я форма потери устойчивости для расчетной схемы с соотношением сторон пластины a/b = 1.0
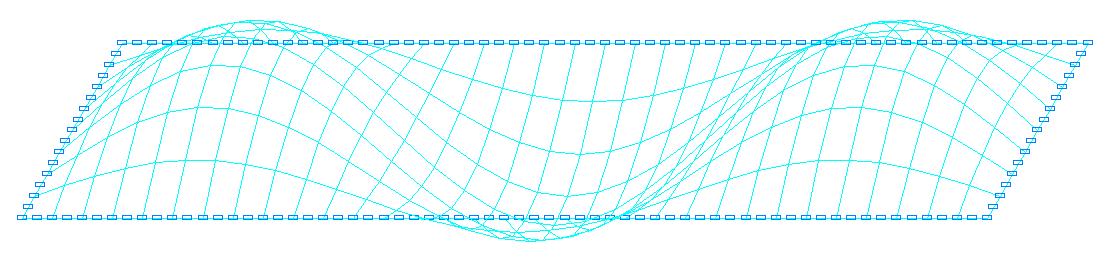
1-я форма потери устойчивости для расчетной схемы с соотношением сторон пластины a/b = 4.0
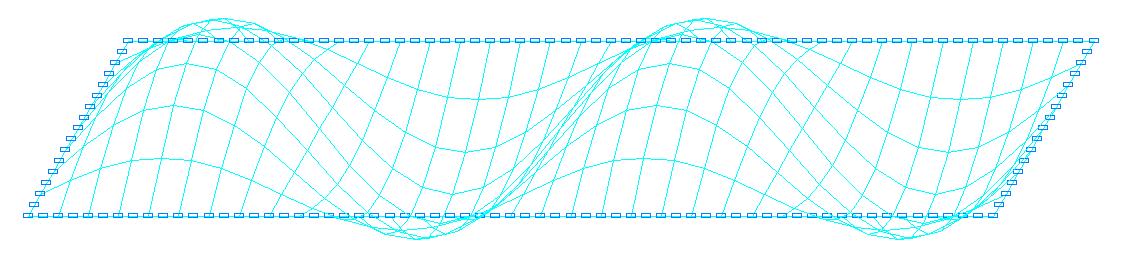
2-я форма потери устойчивости для расчетной схемы с соотношением сторон пластины a/b = 4.0
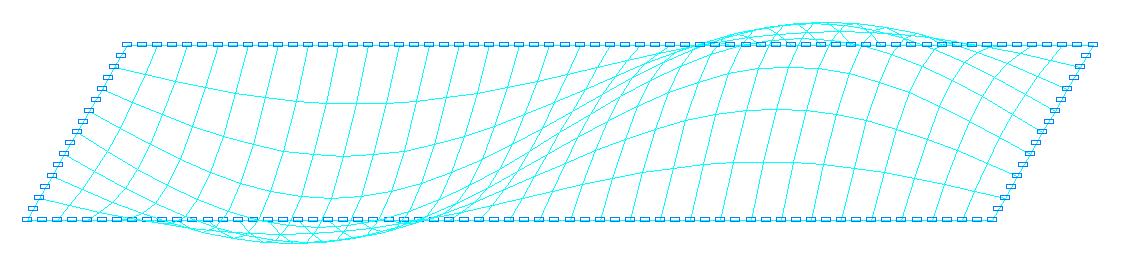
3-я форма потери устойчивости для расчетной схемы с соотношением сторон пластины a/b = 4.0
Сравнение решений:
Критическое значение сжимающих усилий σcrort, кН/м2
|
Расчетная схема |
Форма потери устойчивости |
Количество полуволн в поперечном n и продольном m направлениях |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|---|---|
|
a/b = 1.0 |
1 |
1; 1 |
283093 |
2.831349 ∙1000/0.01 = = 283135 |
0.01 |
|
2 |
1; 2 |
642810 |
6.428985 ∙1000/0.01 = = 642899 |
0.01 |
|
|
3 |
2; 2 |
1132373 |
11.326625 ∙1000/0.01= = 1132663 |
0.03 |
|
|
a/b = 4.0 |
1 |
1; 3 |
264196 |
2.642394 ∙1000/0.01 = = 264239 |
0.02 |
|
2 |
1; 4 |
283093 |
2.831351 ∙1000/0.01 = = 283135 |
0.01 |
|
|
3 |
1; 2 |
334385 |
3.344432 ∙1000/0.01 = = 334443 |
0.02 |
Замечания: При аналитическом решении критическое значение сжимающих усилий σcr, соответствующее моменту потери устойчивости прямоугольной ортотропной пластины, определяется по следующей формуле:
\[\sigma_{crort} =\frac{\pi^{2}\cdot \sqrt {D_{1} \cdot D_{2} } }{b^{2}\cdot h}\cdot \left[ {\sqrt {\frac{D_{1} }{D_{2} }} \cdot \left( {\frac{m\cdot b}{a}} \right)^{2}+\frac{2\cdot D_{3} \cdot n^{2}}{\sqrt {D_{1} \cdot D_{2} } }+\sqrt {\frac{D_{2} }{D_{1} }} \cdot \left( {\frac{n^{2}\cdot a}{m\cdot b}} \right)^{2}} \right], \quad где: \] \[ D_{1} =\frac{E_{x} \cdot h^{3}}{12\cdot \left( {1-\nu_{yx} \cdot \nu_{xy} } \right)}, \quad D_{2} =\frac{E_{y} \cdot h^{3}}{12\cdot \left( {1-\nu_{yx} \cdot \nu_{xy} } \right)}, \] \[ D_{3} =\frac{1}{2}\cdot \left( {D_{1} \cdot \nu_{xy} +D_{2} \cdot \nu_{yx} +4\cdot D_{t} } \right), \quad D_{t} =\frac{G_{xy} \cdot h^{3}}{12}, \]
n, m = 1, 2, 3 … – число полуволн формы потери устойчивости в направлениях поперечном и продольном относительно сжатия пластины.
Жесткостные характеристики ортотропной пластины принимались из условий эквивалентности жесткостным характеристикам подкрепленной пластины из примера 6.10 a:
\[ D_{1} =\frac{E\cdot I}{\frac{b}{s+1}}+\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}, \quad D_{2} =\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}, \quad D_{3} =\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}, \]
и определялись по следующим формулам:
\[ E_{x} =\frac{E}{1-\nu^{2}}\cdot \left[ {\frac{12\cdot \left( {1-\nu^{2}} \right)\cdot I}{h^{3}\cdot \frac{b}{s+1}}+1} \right]\cdot \left[ {1-\frac{\nu^{2}}{\frac{12\cdot \left( {1-\nu^{2}} \right)\cdot I}{h^{3}\cdot \frac{b}{s+1}}+1}} \right], \quad E_{y} =\frac{E}{1-\nu^{2}}\cdot \left[ {1-\frac{\nu^{2}}{\frac{12\cdot \left( {1-\nu^{2}} \right)\cdot I}{h^{3}\cdot \frac{b}{s+1}}+1}} \right], \] \[ \nu_{yx} =\nu , \quad \nu_{xy} =\frac{\nu }{\frac{12\cdot \left( {1-\nu^{2}} \right)\cdot I}{h^{3}\cdot \frac{b}{s+1}}+1}, \quad G_{xy} =\frac{E}{2\cdot \left( {1+\nu } \right)}. \]
Критические значения сжимающих усилий σcr для подкрепленной пластины должны быть уменьшены с коэффициентом k относительно критических значений сжимающих усилий σcr для ортотропной пластины, так как при определении последних не учитывается составляющая, действующая на ребра первой:
\[ k=\frac{b\cdot h}{b\cdot h+F\cdot s}=0.869565, \]
где F — площадь ребра жесткости, s — число ребер.
Критическое значение сжимающих усилий σcr, кН/м2
|
Расчетная схема |
Форма потери устойчивости |
Количество полуволн в поперечном n и продольном m направлениях |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|---|---|
|
a/b = 1.0 |
1 |
1; 1 |
235900 |
283135•0.869565 = = 246204 |
4.37 |
|
2 |
1; 2 |
533934 |
642899•0.869565 = = 559043 |
4.70 |
|
|
3 |
2; 2 |
942681 |
1132663•0.869565 = = 984924 |
4.48 |
|
|
a/b = 4.0 |
1 |
1; 3 |
220165 |
264239•0.869565 = = 229773 |
4.36 |
|
2 |
1; 4 |
235900 |
283135•0.869565 = = 246204 |
4.37 |
|
|
3 |
1; 2 |
278652 |
334443•0.869565 = = 290820 |
4.37 |
