Устойчивость цилиндрической тонкостенной оболочки со свободно опертыми торцами под равномерным внешним давлением
Цель: Определение критического значения внешнего давления, равномерно распределенного по боковой поверхности цилиндрической тонкостенной оболочки, свободно опертой по торцам, соответствующего моменту потери ее устойчивости.
Файл с исходными данными: 6.11_S.spr
Формулировка задачи: Цилиндрическая тонкостенная оболочка, свободно опертая по торцам, находится под воздействием внешнего равномерного давления q. Определить критическое значение внешнего равномерного давления qcr, соответствующее моменту потери устойчивости цилиндрической тонкостенной оболочки.
Ссылки: Э. И. Григолюк, В. В. Кабанов, Устойчивость оболочек, Москва, Наука, 1978, стр. 137.
А. С. Вольмир, Устойчивость деформируемых систем, Москва, Наука, 1967, стр. 545.
Исходные данные:
| E = 2.0·108 кПа | - модуль упругости материала оболочки; |
| ν = 0.3 | - коэффициент Пуассона; |
| h = 0.005 м | - толщина оболочки; |
| R = 0.5 м | - радиус срединной поверхности оболочки; |
| L = 1.0 м | - длина оболочки; |
| q = 1.0·103 кПа | - начальное значение внешнего давления. |
Конечноэлементная модель: Расчетная схема – система общего вида, 1200 четырехузловых элементов оболочки типа 50. Сетка конечных элементов разбита с шагом 0.05 м в меридиональном направлении (20 элементов) и с шагом 6.0º в окружном направлении (60 элементов). Обеспечение граничных условий на свободно опертых торцах достигается за счет наложения связей по направлениям линейных перемещений в их плоскости (степени свободы Y, Z). Геометрическая неизменяемость расчетной схемы обеспечивается за счет наложения связей конечной жесткости (60 элементов типа 51) в узлах поперечного сечения плоскости симметрии цилиндрической оболочки в меридиональном направлении (kx = 1.0 кН/м). На боковой поверхности цилиндрической оболочки задается равномерно распределенная нагрузка (по оси Z1 местной системы координат) с начальным значением q = 1.0·103 кПа. Количество узлов в расчетной схеме – 1260.
Результаты решения в SCAD
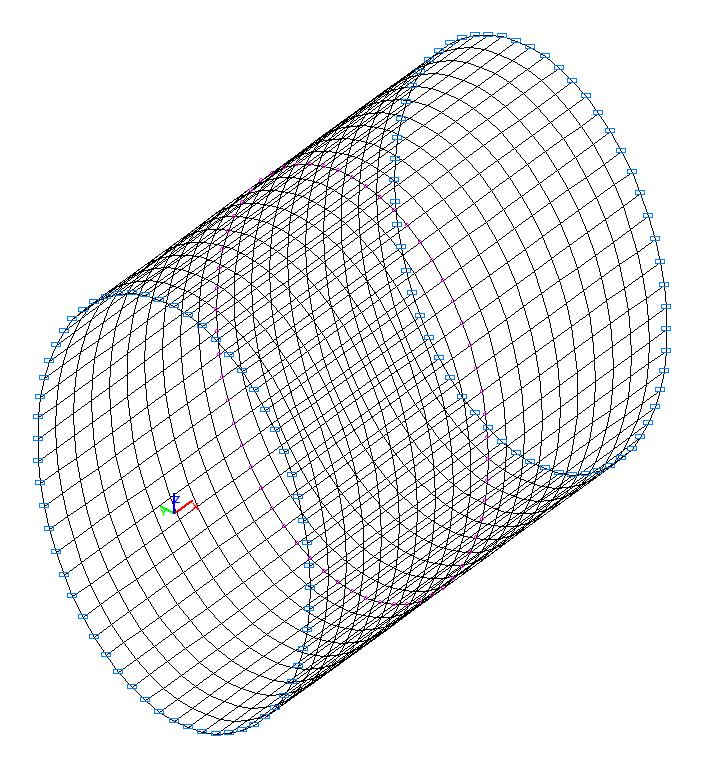
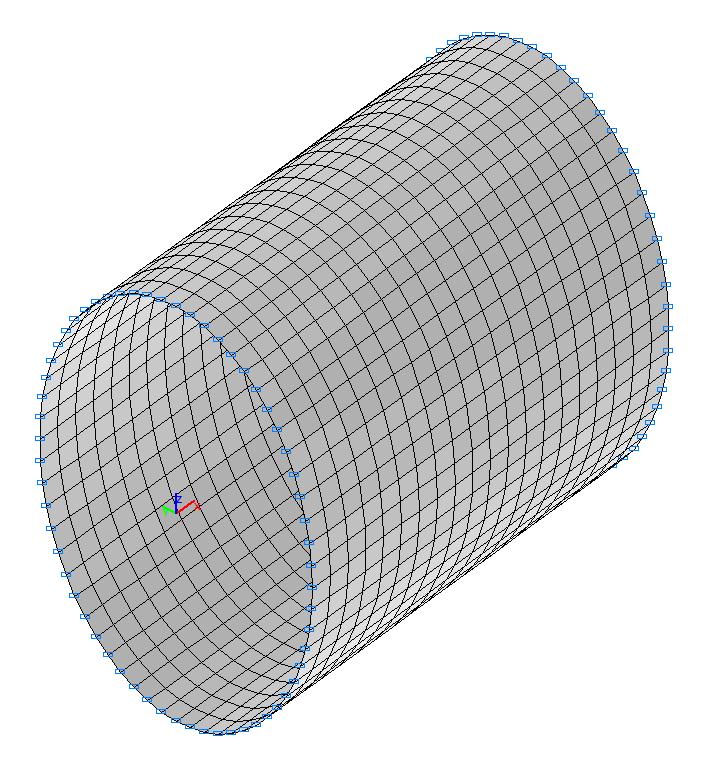
Расчетная схема
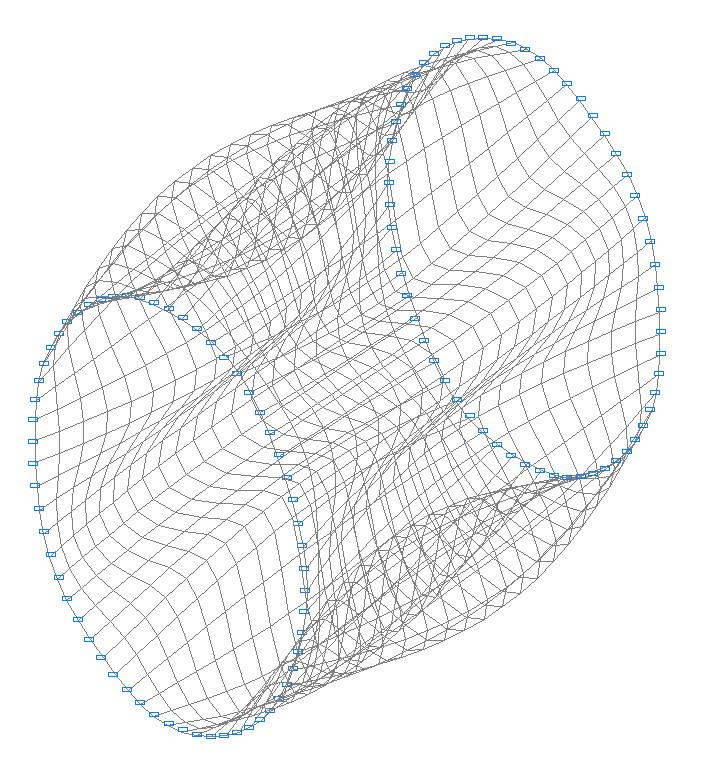
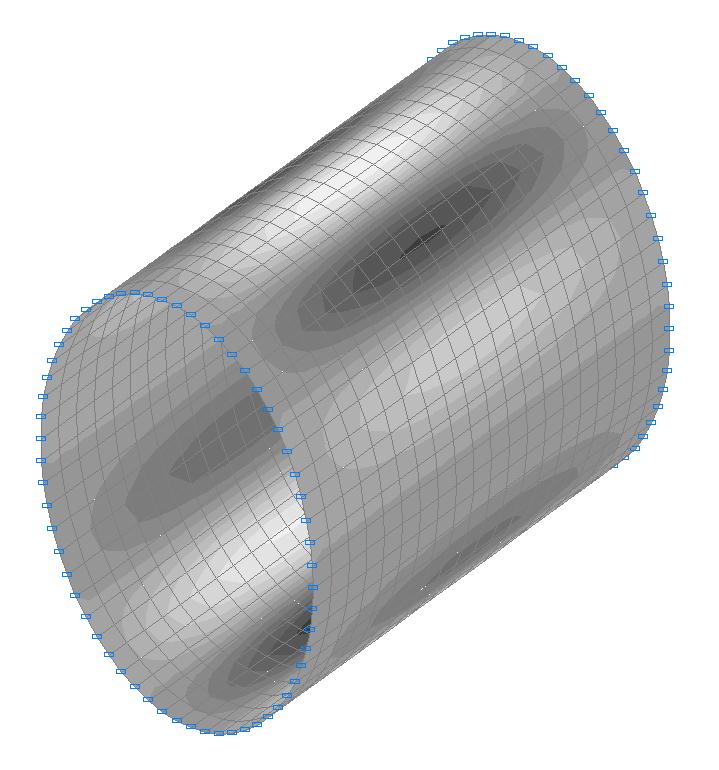
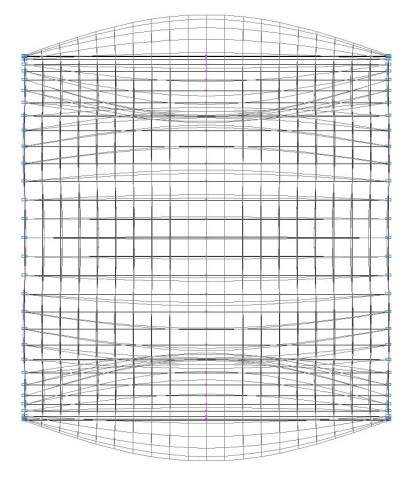
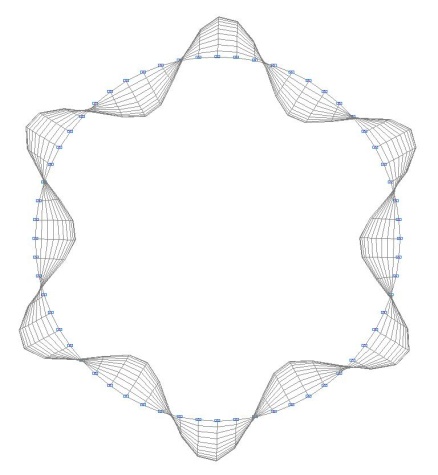
1-я форма потери устойчивости
Сравнение решений:
Критическое значение внешнего равномерного давления qcr, кПа
|
Форма потери устойчивости |
Количество полуволн в меридианальном направлении m и волн в окружном n направлении |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|---|
|
1 |
1; 6 |
981 (917) |
0.999898 ·1000 = = 1000 |
1.94 (9.05) |
Без скобок указаны теоретические значения, посчитанные по теории пологих оболочек для безмоментного исходного состояния;
В круглых скобках указаны теоретические значения, посчитанные по общей теории оболочек для безмоментного исходного состояния.
Замечания: При аналитическом решении критическое значение внешнего равномерного давления qcr, соответствующее моменту потери устойчивости цилиндрической тонкостенной оболочки, определяется в соответствии с теорией пологих оболочек по следующей формуле:
\[ q_{cr} =\frac{E\cdot h}{R\cdot n^{2}}\cdot \frac{\left( {\frac{m\cdot \pi \cdot R}{L}} \right)^{4}}{\left[ {\left( {\frac{m\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right]^{2}}+\frac{D}{R^{3}\cdot n^{2}}\cdot \left[ {\left( {\frac{m\cdot \pi \cdot R}{L}} \right)^{2}+n^{2}} \right]^{2}, \quad где: \] \[ D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}. \]
При аналитическом решении критическое значение внешнего равномерного давления qcr, соответствующее моменту потери устойчивости цилиндрической тонкостенной оболочки, определяется в соответствии с общей теорией оболочек из условия равенства нулю определителя системы разрешающих уравнений:
\[ \left| {{\begin{array}{*{20}c} {\left( {\frac{\pi \cdot R}{L}} \right)^{2}+\frac{1-\nu }{2}\cdot n^{2}+\frac{\left( {1-\nu } \right)^{2}\cdot R}{E\cdot h}\cdot n^{2}\cdot q_{cr} } & {\frac{1+\nu }{2}\cdot \left( {\frac{\pi \cdot R}{L}} \right)\cdot n} & {\nu \cdot \left( {\frac{\pi \cdot R}{L}} \right)} \\ {\frac{1+\nu }{2}\cdot \left( {\frac{\pi \cdot R}{L}} \right)\cdot n} & {\left( {1+\frac{h^{2}}{12\cdot R^{2}}} \right)\cdot \left( {\frac{1-\nu }{2}\cdot \left( {\frac{\pi \cdot R}{L}} \right)^{2}+n^{2}} \right)-\frac{\left( {1-\nu } \right)^{2}\cdot R}{E\cdot h}\cdot n^{2}\cdot q_{cr} } & {\left( {1+\frac{h^{2}}{12\cdot R^{2}}\cdot \left( {\left( {\frac{\pi \cdot R}{L}} \right)^{2}+n^{2}} \right)} \right)\cdot n} \\ {\nu \cdot \left( {\frac{\pi \cdot R}{L}} \right)} & {\left( {1+\frac{h^{2}}{12\cdot R^{2}}\cdot \left( {\left( {\frac{\pi \cdot R}{L}} \right)^{2}+n^{2}} \right)} \right)\cdot n} & {1+\frac{h^{2}}{12\cdot R^{2}}\cdot \left( {\left( {\frac{\pi \cdot R}{L}} \right)^{2}+n^{2}} \right)^{2}-\frac{\left( {1-\nu } \right)^{2}\cdot R}{E\cdot h}\cdot n^{2}\cdot q_{cr} } \\ \end{array} }} \right|=0 \]
