Гибкая длинная прямоугольная пластина, шарнирно опертая по продольным кромкам, под действием поперечной равномерно распределенной нагрузки

Цель: Определение напряженно-деформированного состояния гибкой длинной прямоугольной пластины, шарнирно опертой по продольным кромкам, от воздействия поперечной равномерно распределенной нагрузки.

Файл с исходными данными: nel.spr

Формулировка задачи: Гибкая длинная прямоугольная пластина, шарнирно опертая по продольным кромкам, находится под воздействием поперечной равномерно распределенной по ее площади нагрузки q. Определить поперечное перемещение Z деформированной срединной поверхности, а также максимальные s_yd и минимальные s_yt нормальные напряжения по сечению в половине пролета пластины.

Ссылки: С.П. Тимошенко, С. Войновский-Кригер, Пластины и оболочки, Москва, Физматгиз, 1963, стр. 20.

Исходные данные:

E = 2.1·106 кгс/см2	- модуль упругости;
ν = 0.3	- коэффициент Пуассона;
h = 1.3 см	- толщина пластины;
l = 130.0 cм	- размер короткой стороны пластины (вдоль оси Y общей системы координат);
b = 260.0 cм	- размер элементарной полосы длинной стороны пластины (вдоль оси X общей системы координат);
q = 1.4 кгс/см2	- значение поперечной равномерно распределенной нагрузки.

Конечноэлементная модель: Расчетная  схема  – система общего вида, 1352 элемента плиты типа 341. Сетка конечных элементов разбита по длинам сторон пластины (вдоль осей X, Y общей системы координат) с шагом 5.0 см. Обеспечение граничных условий достигается за счет наложения связей по направлениям степеней свободы X, Y, Z для длинных кромок, расположенных вдоль оси X общей системы координат, из условий шарнирного опирания и по направлениям степеней свободы X, UY для коротких кромок, расположенных вдоль оси Y общей системы координат, из условий цилиндрического изгиба элементарной полосы длинной стороны пластины. Количество узлов в расчетной схеме 1431. Расчет производится в геометрически нелинейной постановке шагово-итерационным методом со следующими параметрами: коэффициент загружения 0.1, количество шагов 10, количество итераций 30.

Результаты решения в SCAD

Расчетная схема

 

Деформированная схема

 

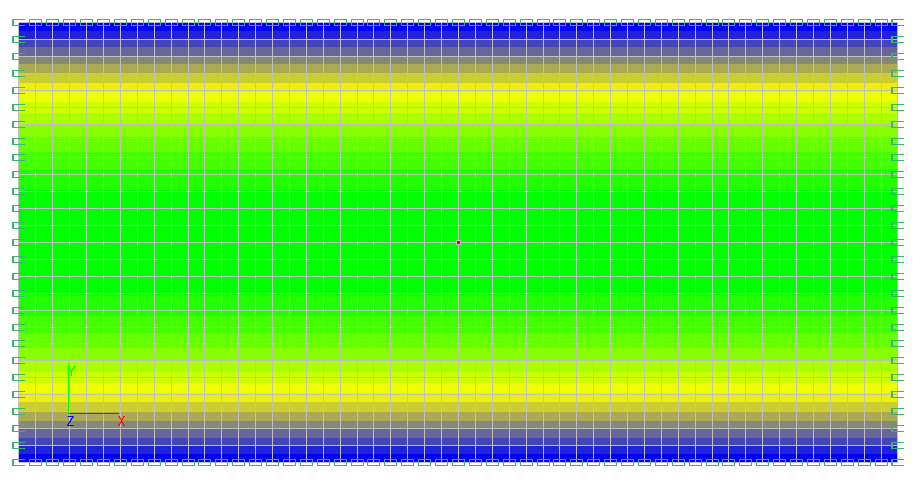
Значения поперечных перемещений Z (см)

 

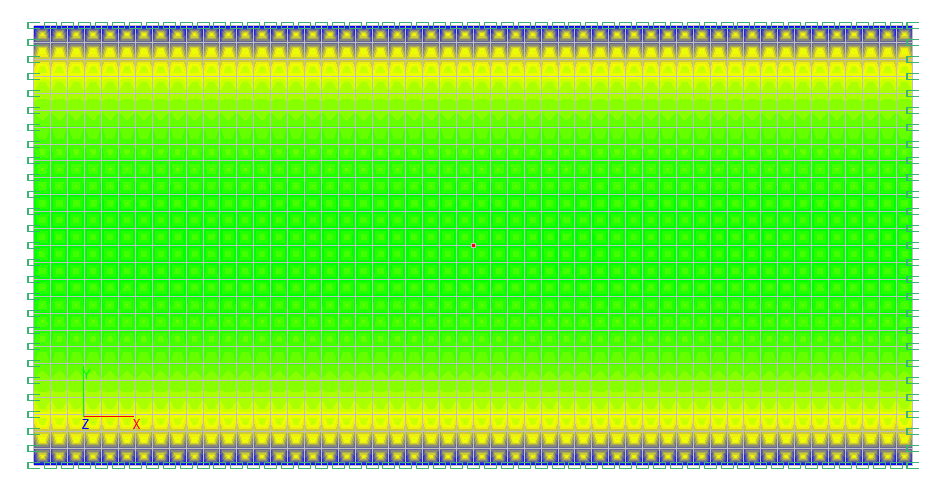
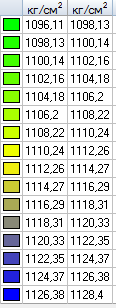
Значения продольных напряжений N_y (кгс/cм²)

 

Эпюра продольных напряжений N_y (кгс/cм²)

 

Значения изгибающих моментов M_y (кгс·см/см)

 

Эпюра изгибающих моментов M_y (кгс·см/см)

 

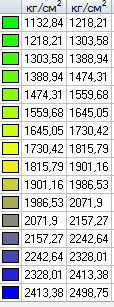
Значения нормальных напряжений s_yd (кгс/см²)

 

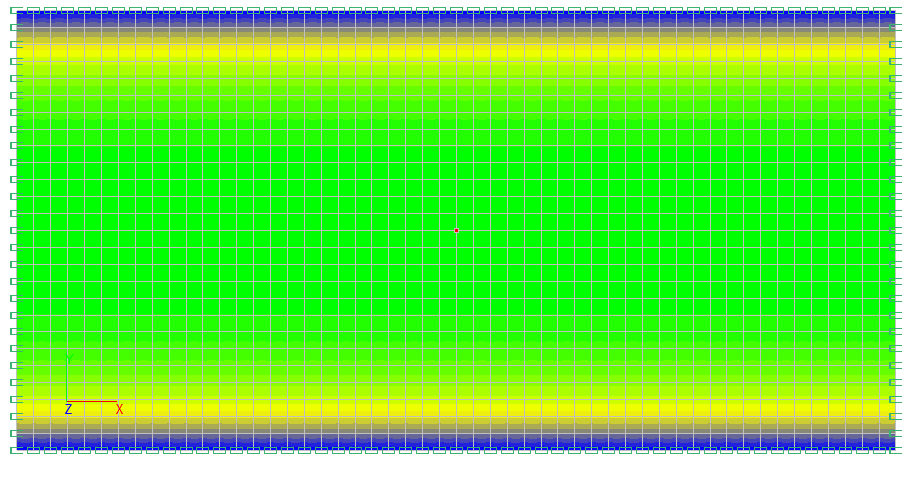
Значения нормальных напряжений s_yt (кгс/см²)

 

Сравнение решений:

Параметр	Теория	SCAD	Отклонения, %
Поперечное перемещение Z деформированной срединной поверхности в половине пролета пластины, см	-1.782	-1.781	0.06
максимальные нормальные напряжения по сечению в половине пролета пластины syd, кгс/см2	2503	2498.7	0.17
минимальные нормальные напряжения по сечению в половине пролета пластины syt, кгс/см2	-287	-294.0	2.44

Замечания: При аналитическом решении перемещение Z деформированной срединной поверхности, а также максимальные s_yd и минимальные s_yt нормальные напряжения по сечению, в половине пролета пластины могут быть вычислены по следующим формулам:

\[ Z=\frac{5\cdot q\cdot l^{4}}{384\cdot D}\cdot \frac{\frac{1}{ch(u)}-1+\frac{u^{2}}{2}}{\frac{5\cdot u^{4}}{24}}; \quad s_{yd} =s_{yN} +s_{yM} ; \quad s_{yt} =s_{yN} -s_{yM} ,  \] \[ где: \quad s_{yN} =\frac{N_{y} }{h}; \quad s_{yM} =\frac{6\cdot M_{y} }{h^{2}}; \quad N_{y} =\frac{4\cdot u^{2}\cdot D}{l^{2}}; \quad M_{y} =\frac{q\cdot l^{2}}{8}\cdot \frac{1-\frac{1}{ch(u)}}{\frac{u^{2}}{2}}; \quad D=\frac{E\cdot h^{3}}{12\cdot \left( {1-\nu^{2}} \right)}. \]

\[ \text { Значение u определяется из выражения:} \quad \frac{E^{2}\cdot h^{8}}{\left( {1-\nu^{2}} \right)^{2}\cdot q^{2}\cdot l^{8}}=\frac{135}{16}\cdot \frac{th(u)}{u^{9}}+\frac{27}{16}\cdot \frac{th^{2}(u)}{u^{8}}-\frac{135}{16\cdot u^{8}}+\frac{9}{8\cdot u^{6}}. \]