Двухвантовая мачта под действием статических нагрузок и сил предварительного натяжения
Цель: Определение напряженного состояния двухвантовой мачты от действия статических нагрузок и сил предварительного натяжения в физически нелинейной постановке.
Файл с исходными данными: Mast.spr
Формулировка задачи: Двухвантовая мачта с заделанным в опоре стволом и симметрично нисходящими от его вершины вантами под углом α к горизонту подвергается следующим воздействиям (в плоскости конструкции мачты):
- В исходном состоянии ванты загружены равномерно распределенной поперечной нагрузкой qlg0 = qrg0 и предварительно напряжены силой H0;
- В рабочем состоянии на ствол мачты действует равномерно распределенная нагрузка qm и момент в вершине Mm, на наветренную и подветренную ванты действуют равномерно распределенные нагрузки qlg и qrg, температура системы не меняется.
Определить продольные силы Nlg, Nrg и Nm в наветренной и в подветренной вантах и в стволе мачты, а также изгибающие моменты Mm в сечениях ствола мачты.
Ссылки: А. В. Перельмутер, Основы расчета вантово-стержневых систем, Стройиздат, 1969, стр. 61
Исходные данные:
| EFg = 0.58·105 т | - продольная жесткость вант; |
| EIm = 0.92·107 т∙м2 | - изгибная жесткость ствола мачты; |
| S = 93.0 м | - высота ствола мачты; |
| L = 115.5 м | - длина хорды вант; |
| α = 45° | - угол наклона вант к горизонту; |
| qlg0 = qrg0 = 22.75∙10-3∙cos(α) =16.087 т/м | - равномерно распределенная поперечная нагрузка на ванты в исходном состоянии; |
| qlg = 37.40∙10-3 - qlg0/ cos(α) = 14.650 т/м | - равномерно распределенная поперечная нагрузка на наветренную ванту в рабочем состоянии; |
| qrg = qrg0/ cos(α) - 8.10∙10-3 = 14.650 т/м | - равномерно распределенная поперечная нагрузка на подветренную ванту в рабочем состоянии; |
| qm = 950.00∙10-3 т/м | - равномерно распределенная поперечная нагрузка на ствол мачты в рабочем состоянии; |
| Mm = 401.00 т∙м | - момент в вершине ствола мачты; |
| H0 = 19.40 т | - силы предварительного напряжения вант. |
Конечноэлементная модель: Расчетная схема – система общего вида. Элементы ствола мачты – 93 стержневых элемента типа 5. Сетка конечных элементов разбита по высоте ствола мачты (вдоль осей X1 местных систем координат) с шагом 1.0 м. Жесткостные характеристики элементов ствола мачты:
EF = 1.00·108 т; EIy = EIz = GIx = 0.92·107 т·м2.
Элементы вант – 2 вантовых элемента типа 308. Обеспечение граничных условий достигается за счет наложения связей на опорные узлы вант по направлениям степеней свободы X, Z и на опорный узел ствола мачты по направлениям степеней свободы X, Z, UY.
Воздействия в исходном состоянии задаются через жесткостные характеристики вантовых элементов:
| γ = 7.84483 т/м3 | - объемный вес вант; |
| E = 2.00·107 т/м2 | - модуль упругости материала вант; |
| ν = 0.3 | - коэффициент Пуассона; |
| H0 = 19.40 т | - силы предварительного напряжения вант; |
| D = 6.0675 см | - наружный диаметр кольцевого поперечного сечения вант; |
| d = 0.0001 см | - внутренний диаметр кольцевого поперечного сечения вант. |
Для контроля значений внутренних усилий в исходном состоянии создается отдельное загружение с вертикальной сосредоточенной нагрузкой минимального значения P0 = 1.00∙10-4 т в вершине ствола мачты.
Воздействия в рабочем состоянии задаются в виде нагрузок:
- поперечной равномерно распределенной в местной системе координат по оси Z1 на вантовые элементы;
- поперечной равномерно распределенной в общей системе координат по оси X на элементы ствола мачты;
- сосредоточенного момента вокруг оси Y общей системы координат на узел вершины ствола мачты.
Нелинейное загружение формировалось для простого шагового метода с коэффициентом загружения 0.1 и количеством шагов 10 для воздействий исходного состояния, с коэффициентом загружения 0.01 и количеством шагов 100 для воздействий рабочего состояния.
Количество узлов в расчетной схеме – 96.
Результаты решения в SCAD
Расчетная схема в исходном состоянии
Расчетная схема в рабочем состоянии
Деформированная схема в исходном состоянии
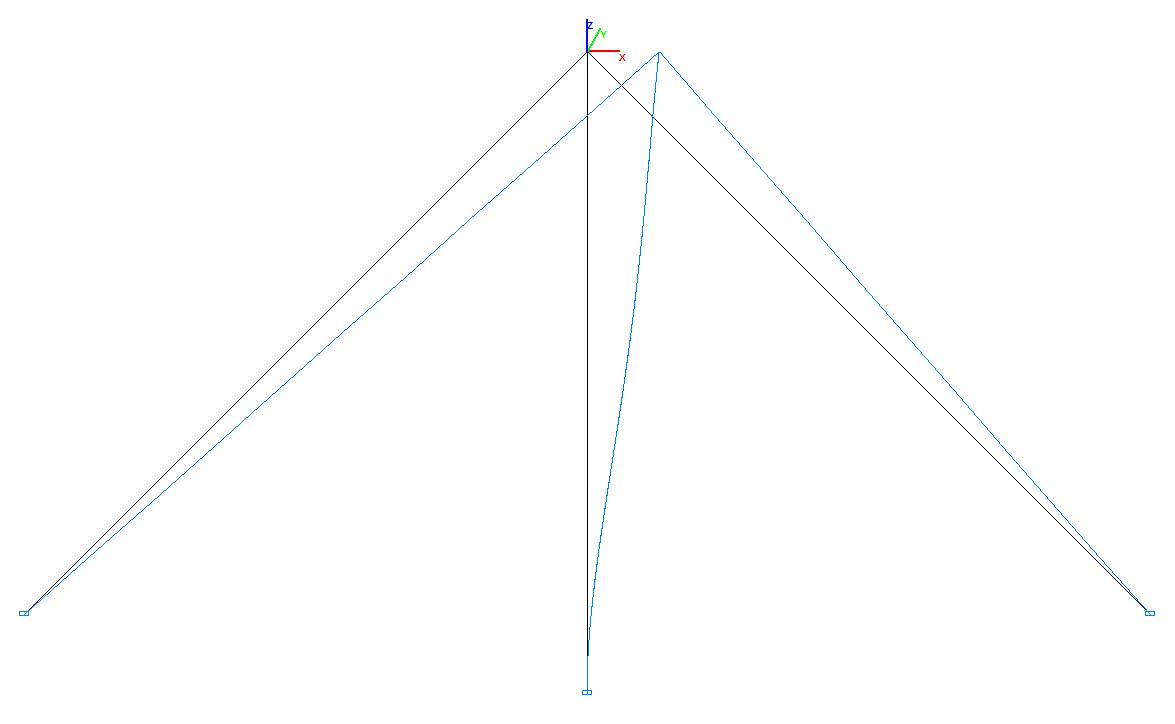
Деформированная схема в рабочем состоянии
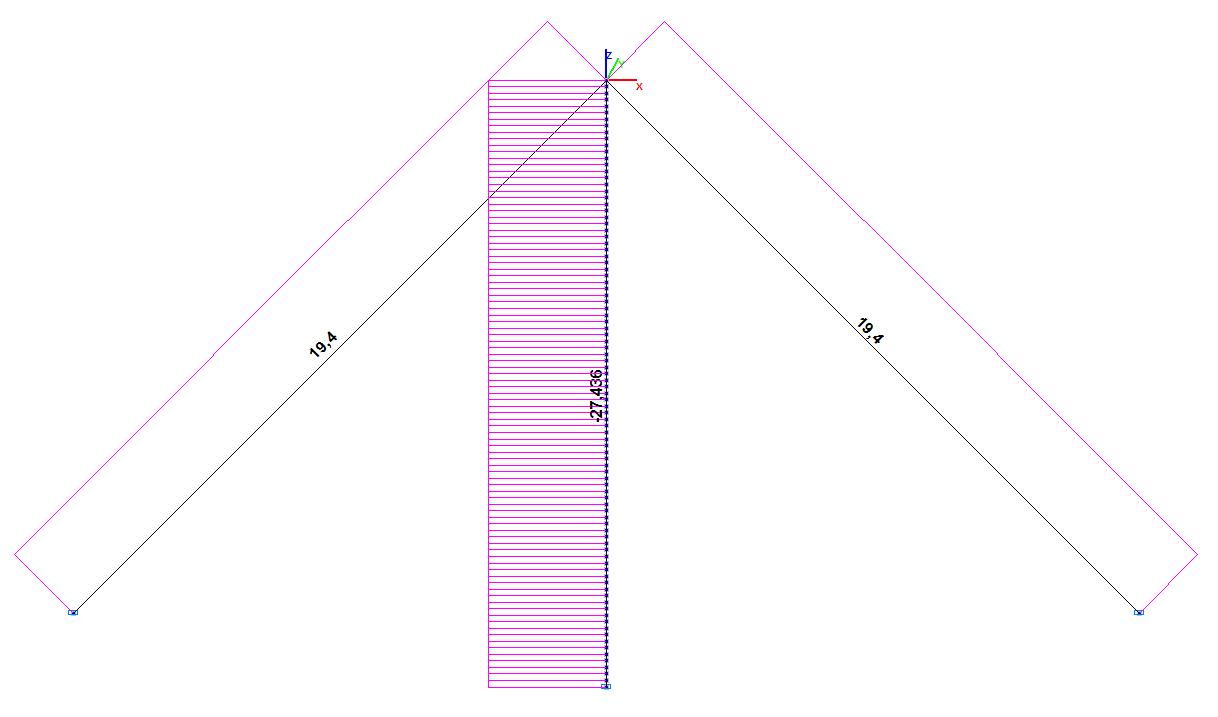
Эпюры продольных сил в исходном состоянии (т)
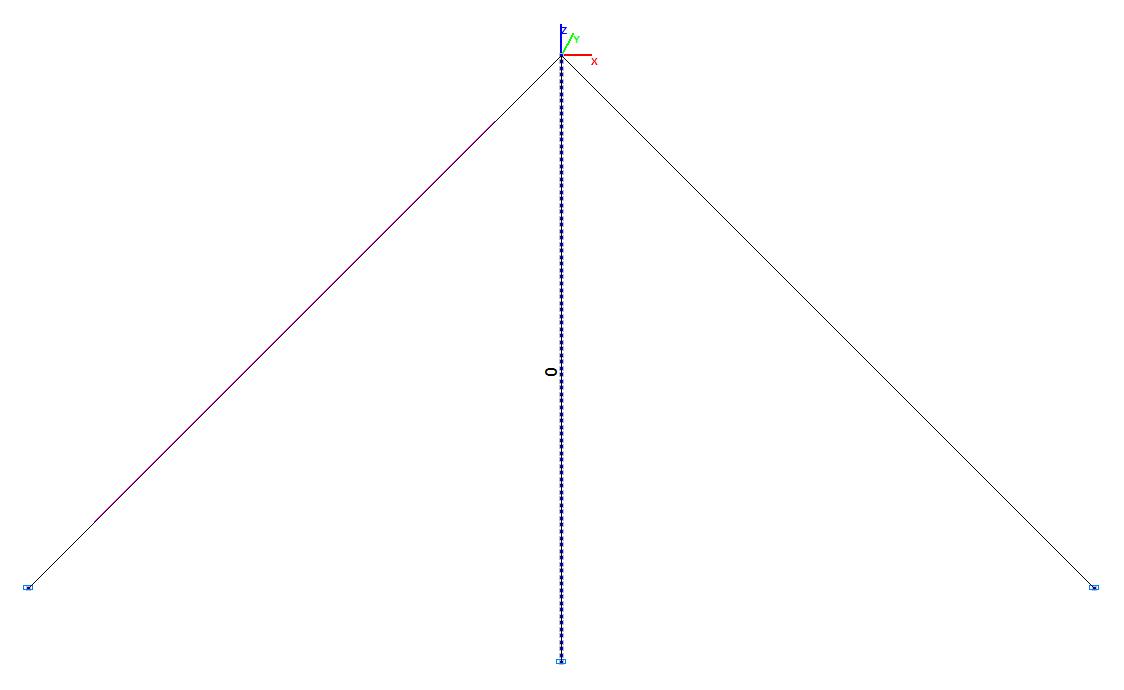
Эпюры изгибающих моментов в исходном состоянии (т∙м)
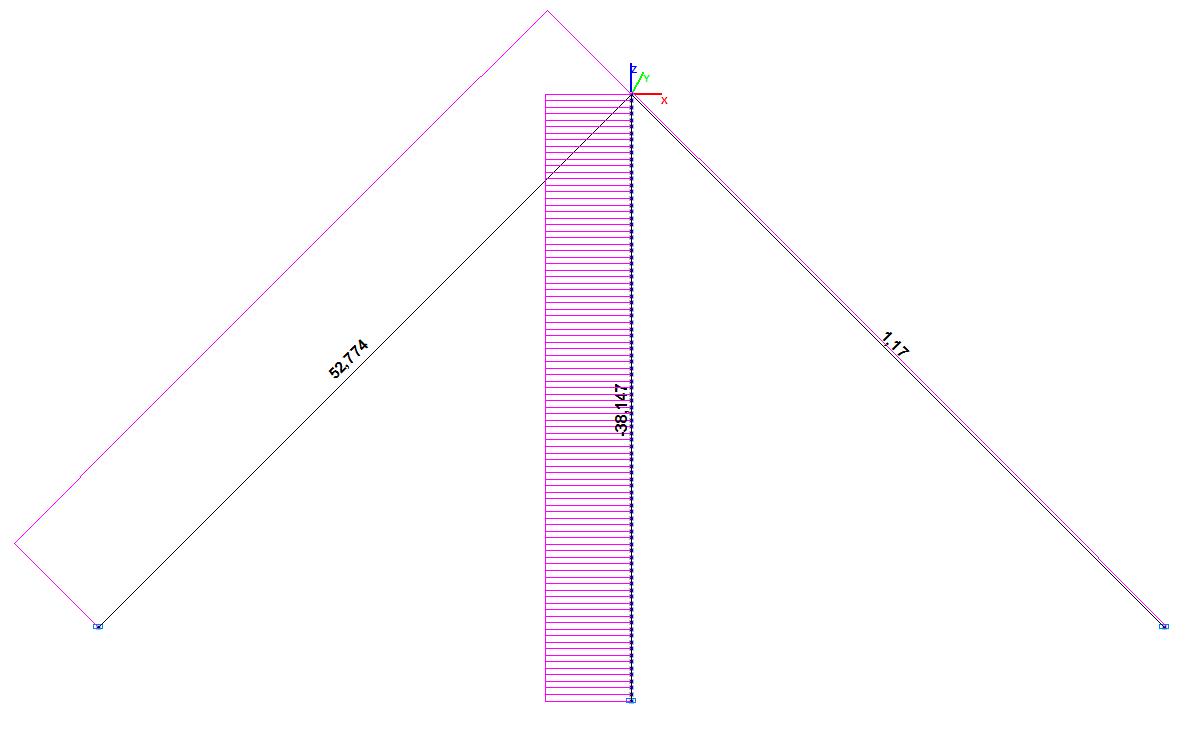
Эпюры продольных сил в рабочем состоянии (т)
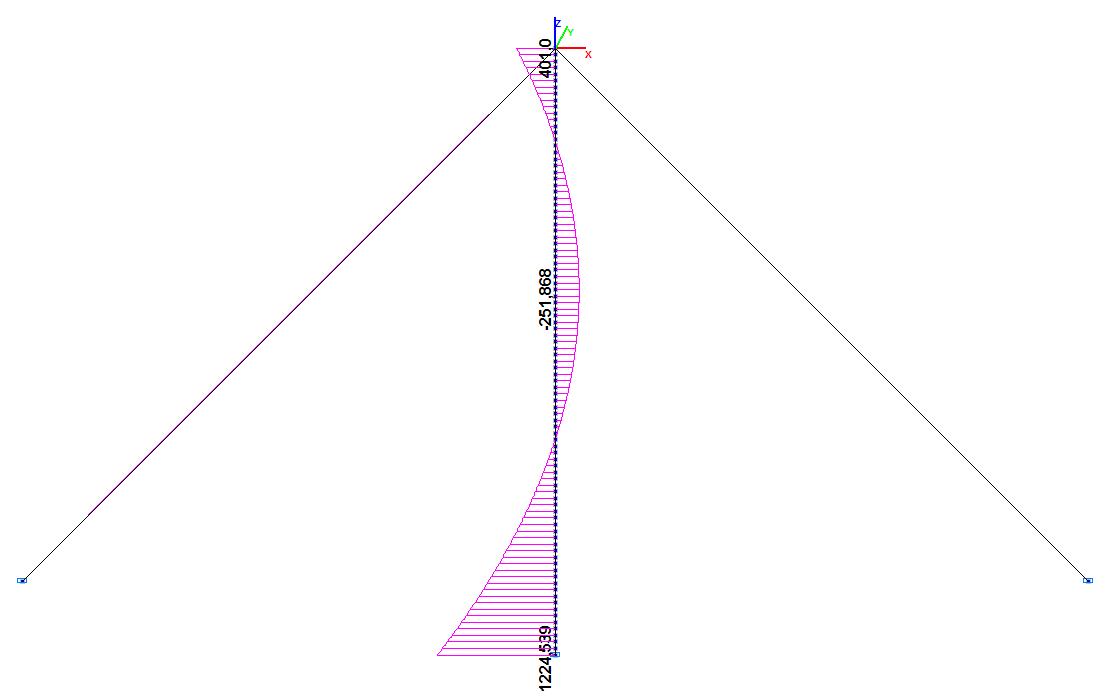
Эпюры изгибающих моментов в рабочем состоянии (т∙м)
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|
|
Nlg, т |
52.769 |
52.774 |
0.01 |
|
Nrg, т |
1.171 |
1.170 |
0.09 |
|
Nm, т |
-38.142 |
-38.147 |
0.01 |
|
Mm(0), т∙м |
1227.376 |
1224.539 |
0.23 |
|
Mm(S), т∙м |
401.000 |
401.000 |
0.00 |
|
Sextr, м |
55.853 |
56.000 |
- |
|
Mm(Sextr), т∙м |
-254.437 |
-251.868 |
1.01 |
Замечания: При аналитическом решении внутренние усилия в дважды статически неопределимой конструкции мачты определяются методом сил, при этом в качестве неизвестных принимаются распорные реакции X1 и X2 опорных узлов вант.
\[ {\begin{array}{*{20}c} {N_{\lg } =H_{0} +N_{\lg 1} \cdot X_{1} +N_{\lg q} ;} \\ {N_{rg} =H_{0} +N_{rg2} \cdot X_{2} +N_{rgq} ;} \\ {N_{m} =-2\cdot H_{0} \cdot \sin \left( \alpha \right)+N_{m1} \cdot X_{1} +N_{m2} \cdot X_{2} +N_{mq} ;} \\ {M_{m} \left( 0 \right)=M_{m1} \left( 0 \right)\cdot X_{1} +M_{m2} \left( 0 \right)\cdot X_{2} +M_{mq} \left( 0 \right);} \\ {M_{m} \left( S \right)=M_{m1} \left( S \right)\cdot X_{1} +M_{m2} \left( S \right)\cdot X_{2} +M_{mq} \left( S \right);} \\ {S_{extr} =S+\frac{q_{\lg } +q_{rg} }{q_{m} }\cdot L\cdot \sin \left( \alpha \right)+\frac{X_{1} -X_{2} }{q_{m} };} \\ {M_{m} \left( {S_{extr} } \right)=\frac{q_{m} }{2}\cdot S_{extr} ^{2}-\left[ {q_{m} \cdot S+\left( {q_{\lg } +q_{rg} } \right)\cdot L\cdot \sin \left( \alpha \right)+X_{1} -X_{2} } \right]\cdot S_{extr} +} \\ {\frac{q_{m} }{2}\cdot S^{2}+\left( {q_{\lg } +q_{rg} } \right)\cdot S\cdot L\cdot \sin \left( \alpha \right)+M_{m} +\left( {X_{1} -X_{2} } \right)\cdot S.} \\ \end{array} } \]
Значения неизвестных X1 и X2 определяются из решения системы линейных уравнений:
\[ \left. {{\begin{array}{*{20}c} {\left( {\frac{N_{\lg 1}^{2}\cdot L}{EF_{g} }+\frac{M_{m1}^{2}\left( 0 \right)\cdot S}{3\cdot EI_{m} }} \right)\cdot X_{1} +\frac{M_{m1} \left( 0 \right)\cdot M_{m2} \left( 0 \right)\cdot S}{3\cdot EI_{m} }\cdot X_{2} +\frac{N_{\lg 1} \cdot N_{\lg q} \cdot L}{EF_{g} }+} \\ {\frac{S}{6\cdot EI_{m} }\cdot \left( {M_{m1} \left( 0 \right)\cdot M_{mq} \left( 0 \right)+4\cdot M_{m1} \left( {\frac{S}{2}} \right)\cdot M_{mq} \left( {\frac{S}{2}} \right)+M_{m1} \left( S \right)\cdot M_{mq} \left( S \right)} \right)-} \\ {\frac{1}{2}\cdot N_{\lg 1} \cdot \left( {\frac{\left( {q_{\lg } +q_{\lg 0} } \right)^{2}\cdot L^{3}}{12\cdot \left( {H_{0} +N_{\lg q} +N_{\lg 1} \cdot X_{1} } \right)^{2}}-\frac{q_{\lg 0}^{2}\cdot L^{3}}{12\cdot H_{0}^{2}}} \right)=0} \\ {\frac{M_{m1} \left( 0 \right)\cdot M_{m2} \left( 0 \right)\cdot S}{3\cdot EI_{m} }\cdot X_{1} +\left( {\frac{N_{rg2}^{2}\cdot L}{EF_{g} }+\frac{M_{m2}^{2}\left( 0 \right)\cdot S}{3\cdot EI_{m} }} \right)\cdot X_{2} +\frac{N_{rg1} \cdot N_{rgq} \cdot L}{EF_{g} }+} \\ {\frac{S}{6\cdot EI_{m} }\cdot \left( {M_{m2} \left( 0 \right)\cdot M_{mq} \left( 0 \right)+4\cdot M_{m2} \left( {\frac{S}{2}} \right)\cdot M_{mq} \left( {\frac{S}{2}} \right)+M_{m2} \left( S \right)\cdot M_{mq} \left( S \right)} \right)-} \\ {\frac{1}{2}\cdot N_{rg2} \cdot \left( {\frac{\left( {-q_{rg} +q_{rg0} } \right)^{2}\cdot L^{3}}{12\cdot \left( {H_{0} +N_{rgq} +N_{rg2} \cdot X_{2} } \right)^{2}}-\frac{q_{rg0}^{2}\cdot L^{3}}{12\cdot H_{0}^{2}}} \right)=0} \\ \end{array} }} \right\}, \quad где: \] \[ N_{\lg 1} =-\frac{1}{\cos \left( \alpha \right)}; \quad N_{m1} =tg\left( \alpha \right); \] \[ M_{m1} \left( 0 \right)=1\cdot S; \quad M_{m1} \left( {\frac{S}{2}} \right)=\frac{S}{2}; \quad M_{m1} \left( S \right)=0\cdot S; \] \[ N_{rg2} =-\frac{1}{\cos \left( \alpha \right)}; \quad N_{m2} =tg\left( \alpha \right); \] \[ M_{m2} \left( 0 \right)=-1\cdot S; \quad M_{m2} \left( {\frac{S}{2}} \right)=-\frac{S}{2}; \quad M_{m2} \left( S \right)=-0\cdot S; \] \[ N_{\lg q} =-\frac{q_{\lg } \cdot L}{2}\cdot tg\left( \alpha \right); \quad N_{rgq} =\frac{q_{rg} \cdot L}{2}\cdot tg\left( \alpha \right); \] \[ N_{mq} =-\frac{\left( {q_{\lg } -q_{rg} } \right)\cdot L}{2}\cdot \frac{\cos \left( {2\cdot \alpha } \right)}{\cos \left( \alpha \right)}; \] \[ M_{mq} \left( 0 \right)=M_{m} +\frac{q_{m} \cdot S^{2}}{2}+\left( {q_{\lg } +q_{rg} } \right)\cdot S\cdot L\cdot \sin \left( \alpha \right); \] \[ M_{mq} \left( {\frac{S}{2}} \right)=M_{m} +\frac{q_{m} \cdot S^{2}}{8}+\frac{\left( {q_{\lg } +q_{rg} } \right)\cdot S\cdot L}{2}\cdot \sin \left( \alpha \right); \] \[ M_{mq} \left( S \right)=M_{m} . \]

