Абсолютно твердое тело, раскрепленное пятью пружинами одинаковой жесткости, работающими только на растяжение, под воздействием сосредоточенной силы
Цель: Определение реакций пружин одинаковой жесткости, работающих только на растяжение и раскрепляющих абсолютно твердое тело от воздействия на него сосредоточенной силы в конструктивно нелинейной постановке.
Файл с исходными данными: Contact_2.spr
Формулировка задачи: Абсолютно твердое тело в форме квадрата со сторонами расположенными вдоль осей координат раскрепляется по углам пятью пружинами одинаковой жесткости, работающими только на растяжение, следующим образом:
- в нижнем левом углу квадрата устанавливаются две пружины (1 и 5), продольные оси которых составляют с нижней стороной квадрата углы 150° и 30° с внешней стороны;
- в верхнем левом углу квадрата устанавливается одна пружина (2), продольная ось которой составляют с верхней стороной квадрата угол 30° с внешней стороны;
- в нижнем правом и в верхнем правом углах квадрата устанавливаются по одной пружине (4 и 3), продольные оси которых составляют соответственно с нижней и с верхней сторонами квадрата углы 90° с внешней стороны.
Перпендикулярно середине левой стороны квадрата абсолютно твердого тела прикладывается сосредоточенная сила P.
Определить реакции в пружинах Ri.
Ссылки: А. В. Перельмутер, В. И. Сливкер, Расчетные модели сооружений и возможность их анализа, Москва, СКАД СОФТ, 2011, стр. 147
Исходные данные:
| L = 20 м | - сторона квадрата абсолютно твердого тела; |
| α1 = 150° | - угол наклона оси пружины 1 к нижней стороне квадрата с внешней стороны; |
| α2 = 30° | - угол наклона оси пружины 2 к верхней стороне квадрата с внешней стороны; |
| α3 = 90° | - угол наклона оси пружины 3 к верхней стороне квадрата с внешней стороны; |
| α4 = 90° | - угол наклона оси пружины 4 к нижней стороне квадрата с внешней стороны; |
| α5 = 30° | - угол наклона оси пружины 5 к нижней стороне квадрата с внешней стороны; |
| k = 1.00·106 кН/м | - продольная жесткость пружин; |
| P = 10.0 кН | - значение сосредоточенной силы, действующей перпендикулярно середине левой стороны квадрата. |
Конечноэлементная модель: Расчетная схема – плоская рама. Элемент абсолютно твердого тела – 1 элемент трехмерного шестиузлового твердого тела типа 100 (один ведущий узел, расположенный на пересечении диагоналей квадрата, четыре ведомых узла, расположенных по углам квадрата, один ведомый узел, расположенный на середине левой стороны квадрата). Элементы пружин – 5 элементов односторонних двухузловых связей типа 352. Обеспечение граничных условий достигается за счет наложения связей на опорные узлы пружин по направлениям степеней свободы X, Z. Для обеспечения геометрической неизменяемости системы в ходе нелинейного расчета в ведущий узел твердого тела вводится элемент связи конечной жесткости (типа 51) малого значения 0.001 кН/м по направлению оси X общей системы координат. Правильность результатов расчета контролируется отсутствием реакции в этой связи. Воздействие задается в виде узловой нагрузки P (по направлению оси X общей системы координат). Нелинейное загружение формировалось для шагово-итерационного метода с коэффициентом загружения - 1, количеством шагов - 1, количеством итераций - 10 для линейного загружения P. Количество узлов в расчетной схеме – 17.
Результаты решения в SCAD
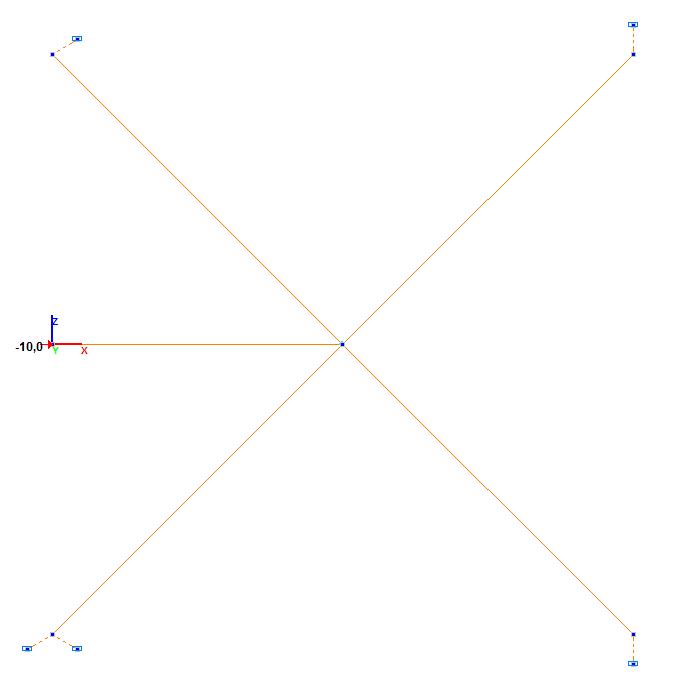
Расчетная схема
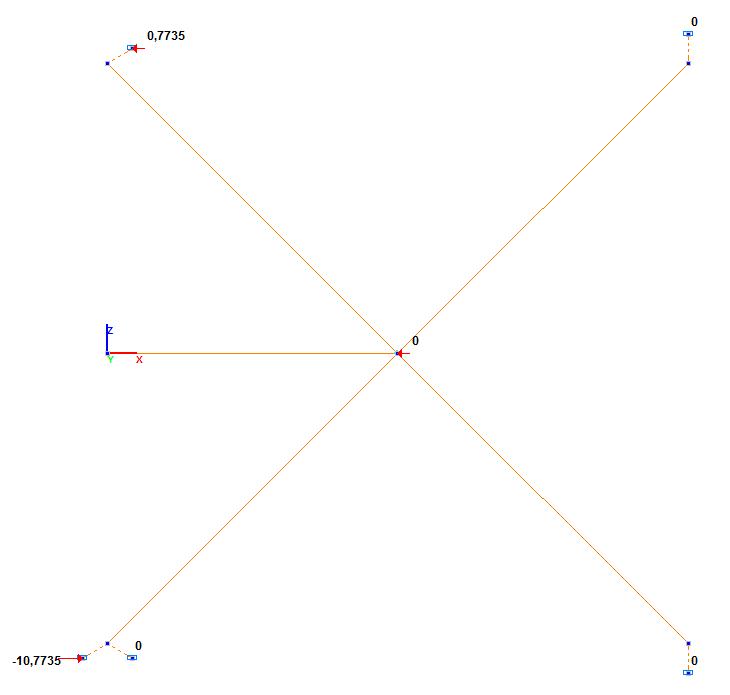
Значения реакций в опорных узлах пружин вдоль оси X общей системы координат Rx, кН
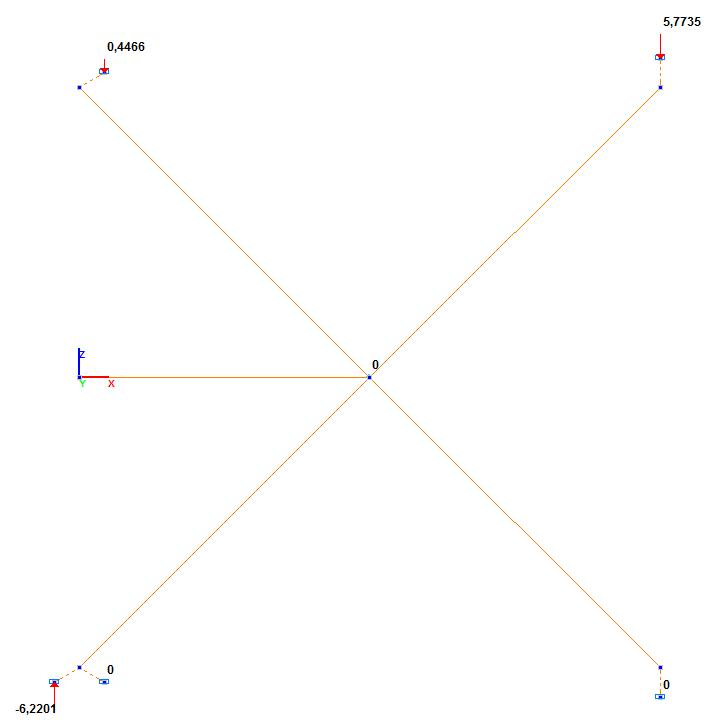
Значения реакций в опорных узлах пружин вдоль оси Z общей системы координат Rz, кН
Сравнение решений:
|
Параметр |
Теория |
SCAD |
Отклонение, % |
|---|---|---|---|
|
R1, кН |
12.440 |
-10.7735•cos150° + 6.2201•sin150° = 12.440 |
0.00 |
|
R2, кН |
0.893 |
0.7735•cos30° + 0.4466•sin30° = 0.893 |
0.00 |
|
R3, кН |
5.770 |
5.7735•sin90° = 5.774 |
0.07 |
|
R4, кН |
0.000 |
0.000 |
0.00 |
|
R5, кН |
0.000 |
0.000 |
0.00 |
Замечания: При аналитическом решении реакции в пружинах Ri определяются методом квадратичного программирования.
