Геометрические характеристики замкнутого тонкостенного эллиптического сечения
Цель: Проверка точности вычислений геометрических характеристик замкнутой эллиптической оболочки поперечного сечения стержня.
Формулировка задачи: Для замкнутой эллиптической оболочки поперечного сечения стержня проверить точность вычислений геометрических характеристик.
Ссылки: А. А. Уманский, Справочник проектировщика промышленных, жилых и общественных зданий и сооружений. Расчетно-теоретический. Книга 1, Москва, Стройиздат, 1972.
А.В. Александров, В.Д. Потапов, Б.П. Державин, Сопротивление материалов, Москва, Высшая школа, 1995.
Исходные данные:
| a = 50 см | - размер большой полуоси эллиптической оболочки поперечного сечения (вдоль оси Y); |
| b = 30 см | - размер малой полуоси эллиптической оболочки поперечного сечения (вдоль оси Z); |
| t = 1.0 см | - толщина оболочки поперечного сечения. |
Файл с исходными данными: Ellipse_Shell.tns
Расчетная модель: Расчетная модель образуется на основе модели срединного контура, импортируемого из графического редактора AutoCAD. Модель контура представляет собой многоугольник, вписанный в эллипс с заданными характеристиками и построенный в полярных координатах с шагом угла φ = 3°. Количество вершин многоугольника в модели – 120.
Результаты решения в Тонус
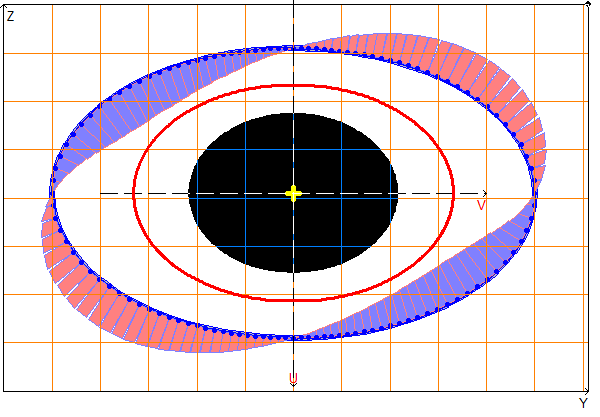
Расчетная модель, главные оси, центр масс, эллипс инерции, ядро сечения, эпюры секториальных площадей
Сравнение решений:
|
Параметр |
Теория |
ТОНУС |
Отклонение, % |
|---|---|---|---|
|
Площадь поперечного сечения, A см2 |
255.180 |
255.215 |
0.01 |
|
Условная площадь среза вдоль главной оси U, Av,y см2 |
81.383 |
80.890 |
0.61 |
|
Условная площадь среза вдоль главной оси V, Av,z см2 |
173.738 |
174.325 |
0.34 |
|
Угол наклона главных осей инерции, α рад |
1.5708 |
1.5708 |
0.00 |
|
Момент инерции относительно центральной оси Y1, параллельной оси Y, Iy см4 |
128657.250 |
128839.668 |
0.14 |
|
Момент инерции относительно центральной оси Z1, параллельной оси Z, Iz см4 |
280418.750 |
279824.429 |
0.21 |
|
Момент инерции при свободном кручении, It см4 |
348176.760 |
347677.226 |
0.14 |
|
Секториальный момент инерции, Iw см6 |
4265014.702 |
4260080.440 |
0.12 |
|
Радиус инерции относительно оси Y1, iy см |
22.457 |
22.468 |
0.05 |
|
Радиус инерции относительно оси Z1, iz см |
33.154 |
33.112 |
0.13 |
|
Максимальный момент сопротивления относительно оси U, Wu+ см3 |
5608.375 |
5541.222 |
1.20 |
|
Минимальный момент сопротивления относительно оси U, Wu- см3 |
5608.375 |
5541.222 |
1.20 |
|
Максимальный момент сопротивления относительно оси V, Wv+ см3 |
4288.575 |
4224.254 |
1.50 |
|
Минимальный момент сопротивления относительно оси V, Wv- см3 |
4288.575 |
4224.254 |
1.50 |
|
Пластический момент сопротивления относительно оси U, Wpl,u см3 |
7471.878 |
7467.234 |
0.06 |
|
Пластический момент сопротивления относительно оси V, Wpl,v см3 |
5277.357 |
5275.030 |
0.04 |
|
Максимальный момент инерции, Iu см4 |
280418.750 |
279824.429 |
0.21 |
|
Минимальный момент инерции, Iv см4 |
128657.250 |
128839.668 |
0.14 |
|
Максимальный радиус инерции, iu см |
33.154 |
33.112 |
0.13 |
|
Минимальный радиус инерции, iv см |
22.457 |
22.468 |
0.05 |
|
Ядровое расстояние вдоль положительного направления оси Y (U), a u+ см |
16.810 |
16.552 |
1.53 |
|
Ядровое расстояние вдоль отрицательного направления оси Y (U), a u- см |
16.810 |
16.552 |
1.53 |
|
Ядровое расстояние вдоль положительного направления оси Z (V), a v+ см |
21.983 |
21.712 |
1.23 |
|
Ядровое расстояние вдоль отрицательного направления оси Z (V), a v- см |
21.983 |
21.712 |
1.23 |
|
Координата центра масс по оси Y, ym см |
0.000 |
0.000 |
— |
|
Координата центра масс по оси Z, zm см |
0.000 |
0.000 |
— |
|
Координата центра изгиба по оси Y, yb см |
0.000 |
0.013 |
— |
|
Координата центра изгиба по оси Z, zb см |
0.000 |
0.040 |
— |
|
Периметр, P см |
510.360 |
510.430 |
0.01 |
|
Внутренний периметр, Pi см |
255.180 |
255.215 |
0.01 |
|
Внешний периметр, Pe см |
255.180 |
255.215 |
0.01 |
|
Полярный момент инерции, Ip см4 |
409076.000 |
408664.097 |
0.10 |
|
Полярный радиус инерции, ip см |
40.043 |
40.016 |
0.07 |
|
Полярный момент сопротивления, Wp см3 |
8181.520 |
8092.567 |
1.09 |
Значения эпюры секториальных площадей ω в первой четверти декартовой системы координат UV, см2
|
φ, ° |
Теория |
ТОНУС |
Отклонение, % |
|---|---|---|---|
|
0 |
0.000 |
0.000 |
0.00 |
|
3 |
-33.798 |
-33.931 |
0.39 |
|
6 |
-66.041 |
-66.277 |
0.36 |
|
9 |
-95.381 |
-95.675 |
0.31 |
|
12 |
-120.827 |
-121.132 |
0.25 |
|
15 |
-141.807 |
-142.088 |
0.20 |
|
18 |
-158.147 |
-158.383 |
0.15 |
|
21 |
-169.998 |
-170.171 |
0.11 |
|
24 |
-177.691 |
-177.821 |
0.07 |
|
27 |
-181.736 |
-181.819 |
0.05 |
|
30 |
-182.648 |
-182.691 |
0.02 |
|
33 |
-180.947 |
-180.957 |
0.01 |
|
36 |
-177.108 |
-177.094 |
0.01 |
|
39 |
-171.555 |
-171.521 |
0.02 |
|
42 |
-164.646 |
-164.598 |
0.03 |
|
45 |
-156.680 |
-156.624 |
0.04 |
|
48 |
-147.904 |
-147.842 |
0.04 |
|
51 |
-138.514 |
-138.448 |
0.05 |
|
54 |
-128.666 |
-128.599 |
0.05 |
|
57 |
-118.482 |
-118.417 |
0.05 |
|
60 |
-108.058 |
-107.995 |
0.06 |
|
63 |
-97.466 |
-97.407 |
0.06 |
|
66 |
-86.761 |
-86.706 |
0.06 |
|
69 |
-75.982 |
-75.933 |
0.06 |
|
72 |
-65.158 |
-65.115 |
0.07 |
|
75 |
-54.310 |
-54.273 |
0.07 |
|
78 |
-43.450 |
-43.420 |
0.07 |
|
81 |
-32.586 |
-32.564 |
0.07 |
|
84 |
-21.722 |
-21.707 |
0.07 |
|
87 |
-10.861 |
-10.853 |
0.07 |
|
90 |
0.000 |
0.000 |
0.00 |
Замечания: При аналитическом решении геометрические характеристики замкнутой эллиптической оболочки поперечного сечения стержня определяются по следующим формулам:
\[ A=4\cdot t\cdot a\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right); \] \[ A_{v,y} =4\cdot t\cdot \frac{a\cdot b^{2}}{a^{2}-b^{2}}\cdot \left[ {F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)-E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right]; \] \[ A_{v,z} =4\cdot t\cdot \frac{a}{a^{2}-b^{2}}\cdot \left[ {a^{2}\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)-b^{2}\cdot F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right]; \] \[ \alpha =0; \] \[ \mbox{I}_{\mbox{y}} =I_{v} =I_{1} =\frac{4}{3}\cdot t\cdot \frac{a\cdot b^{2}}{a^{2}-b^{2}}\cdot \left[ {\left( {2\cdot a^{2}-b^{2}} \right)\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)-b^{2}\cdot F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right]; \] \[ \mbox{I}_{\mbox{z}} =I_{u} =I_{2} =\frac{4}{3}\cdot t\cdot \frac{a^{3}}{a^{2}-b^{2}}\cdot \left[ {\left( {a^{2}-2\cdot b^{2}} \right)\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)+b^{2}\cdot F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right]; \] \[ I_{t} =\frac{\pi^{2}\cdot t\cdot a\cdot b^{2}}{E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}; \] \[ \omega =a\cdot b\cdot \left[ {\arcsin \left( {\frac{v}{a}} \right)-\frac{\pi }{2}\cdot \frac{E\left( {\arcsin \left( {\frac{v}{a}} \right);\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}{E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}} \right]; \] \[ v=\frac{a\cdot b\cdot \cos \left( \phi \right)}{\sqrt {a^{2}\cdot \sin ^{2}\left( \phi \right)-b^{2}\cdot \cos^{2}\left( \phi \right)} }; \] \[ {\begin{array}{*{20}c} {I_{\omega } \approx \frac{\pi^{2}\cdot t\cdot a^{3}\cdot b^{2}}{E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}\cdot \left[ {0.007812500\cdot \frac{\left( {a^{2}-b^{2}} \right)^{2}}{a^{4}}+0.003906250\cdot \frac{\left( {a^{2}-b^{2}} \right)^{3}}{a^{6}}+} \right.} \\ {+0.002326965\cdot \frac{\left( {a^{2}-b^{2}} \right)^{4}}{a^{8}}+0.001537323\cdot \frac{\left( {a^{2}-b^{2}} \right)^{5}}{a^{10}}+0.001087957\cdot \frac{\left( {a^{2}-b^{2}} \right)^{6}}{a^{12}}+} \\ {+0.000808729\cdot \frac{\left( {a^{2}-b^{2}} \right)^{7}}{a^{14}}+0.000254599\cdot \frac{\left( {a^{2}-b^{2}} \right)^{8}}{a^{16}}+0.000113341\cdot \frac{\left( {a^{2}-b^{2}} \right)^{9}}{a^{18}}+} \\ {\left. {+0.000053772\cdot \frac{\left( {a^{2}-b^{2}} \right)^{10}}{a^{20}}+0.000024374\cdot \frac{\left( {a^{2}-b^{2}} \right)^{11}}{a^{22}}+0.000008701\cdot \frac{\left( {a^{2}-b^{2}} \right)^{12}}{a^{24}}} \right]} \\ \end{array} }; \] \[ i_{y} =i_{v} =\sqrt {\frac{b^{2}}{3\cdot \left( {a^{2}-b^{2}} \right)}\cdot \left\{ {2\cdot a^{2}-b^{2}\cdot \left[ {1+\frac{F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}{E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}} \right]} \right\}} ; \] \[ i_{z} =i_{u} =\sqrt {\frac{a^{2}}{3\cdot \left( {a^{2}-b^{2}} \right)}\cdot \left\{ {a^{2}-2\cdot b^{2}\cdot \left[ {1-\frac{F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}{2\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}} \right]} \right\}} ; \] \[ W_{u+} =W_{u-} =\frac{4}{3}\cdot t\cdot \frac{a^{2}}{a^{2}-b^{2}}\cdot \left[ {\left( {a^{2}-2\cdot b^{2}} \right)\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)+b^{2}\cdot F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right]; \] \[ W_{v+} =W_{v-} =\frac{4}{3}\cdot t\cdot \frac{a\cdot b}{a^{2}-b^{2}}\cdot \left[ {\left( {2\cdot a^{2}-b^{2}} \right)\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)-b^{2}\cdot F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right]; \] \[ W_{pl,u} =2\cdot t\cdot a\cdot \left[ {a+\frac{b^{2}}{\sqrt {a^{2}-b^{2}} }\cdot \ln \left| {\frac{\sqrt {a^{2}-b^{2}} +a}{b}} \right|} \right]; \] \[ W_{pl,v} =2\cdot t\cdot b\cdot \left[ {b+\frac{a^{2}}{\sqrt {a^{2}-b^{2}} }\cdot \arcsin \left( {\frac{\sqrt {a^{2}-b^{2}} }{b}} \right)} \right]; \] \[ a_{u+} =a_{u-} =\frac{1}{3}\cdot \frac{b}{a^{2}-b^{2}}\cdot \left\{ {2\cdot a^{2}-b^{2}\cdot \left[ {1+\frac{F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}{E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}} \right]} \right\}; \] \[ a_{v+} =a_{v-} =\frac{1}{3}\cdot \frac{a}{a^{2}-b^{2}}\cdot \left\{ {a^{2}-2\cdot b^{2}\cdot \left[ {1-\frac{F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}{2\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}} \right]} \right\}; \] \[ y_{m} =y_{b} =z_{m} =z_{b} =0; \] \[ P_{e} =P_{i} =4\cdot a\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right); \quad P=P_{e} +P_{i} ; \] \[ I_{12} =0; \] \[ I_{p} =\frac{4}{3}\cdot t\cdot a\cdot \left[ {\left( {a^{2}+b^{2}} \right)\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)+b^{2}\cdot F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right]; \] \[ i_{p} =\sqrt {\frac{1}{3}\cdot \left\{ {a^{2}+b^{2}\cdot \left[ {1+\frac{F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}{E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}} \right]} \right\}} ; \] \[ W_{p} =\frac{4}{3}\cdot t\cdot \left[ {\left( {a^{2}+b^{2}} \right)\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)+b^{2}\cdot F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right], \]
где:F(x) - полный эллиптический интеграл Лежандра первого рода,
E(x) - полный эллиптический интеграл Лежандра второго рода,
E(k,x) - неполный эллиптический интеграл Лежандра второго рода.