Секториальные площади, статические моменты и касательные напряжения для тонкостенного открыто-замкнутого многоконтурного сечения

Цель: Проверка точности определения секториальных площадей ω, статических моментов относительно главных осей инерции сечения S_u, S_v, секториального статического момента S_ω, касательных напряжений τ_u, τ_v, обусловленных действием поперечных сил, а также касательных напряжений τ_ω, обусловленных стесненным кручением для тонкостенного открыто-замкнутого многоконтурного сечения.

Имя файла с исходными данными: Prokic_openclosed.tns

Формулировка задачи: Для тонкостенного открыто-замкнутого многоконтурного поперечного сечения проверить точность вычисления секториальных площадей, статических моментов и касательных напряжений.

Ссылки: Prokić A. Computer program for determination of geometrical properties of thin-walled beams with open-closed section // Computers and Structures, Vol. 74 (2000). – pp. 705 – 715.

Исходные данные:

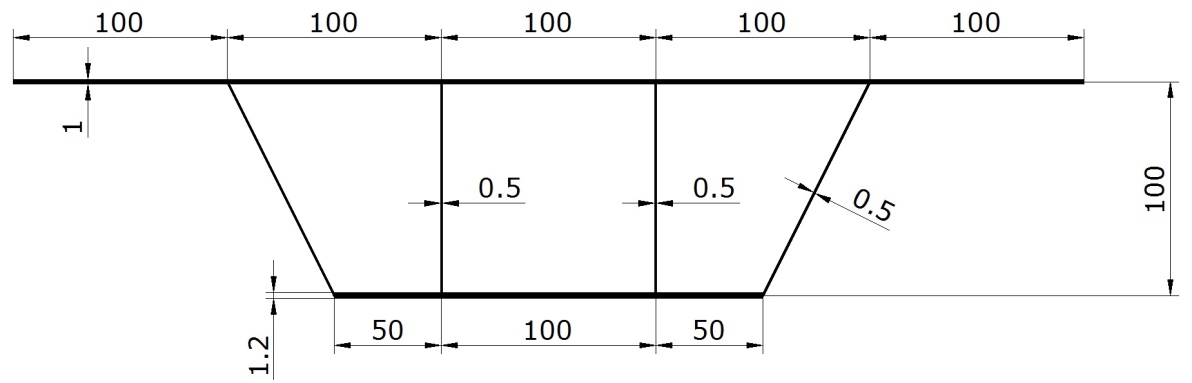
Многоконтурное открыто-замкнутое тонкостенное сечение с размерами, см

 

Результаты решения из источника:

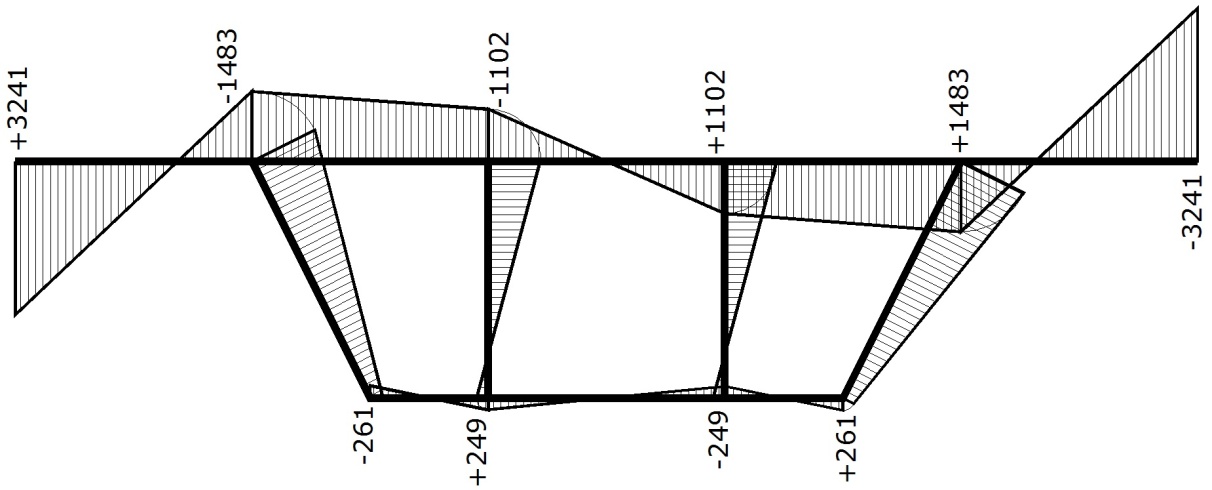
Эпюра секториальных площадей ω, см²

 

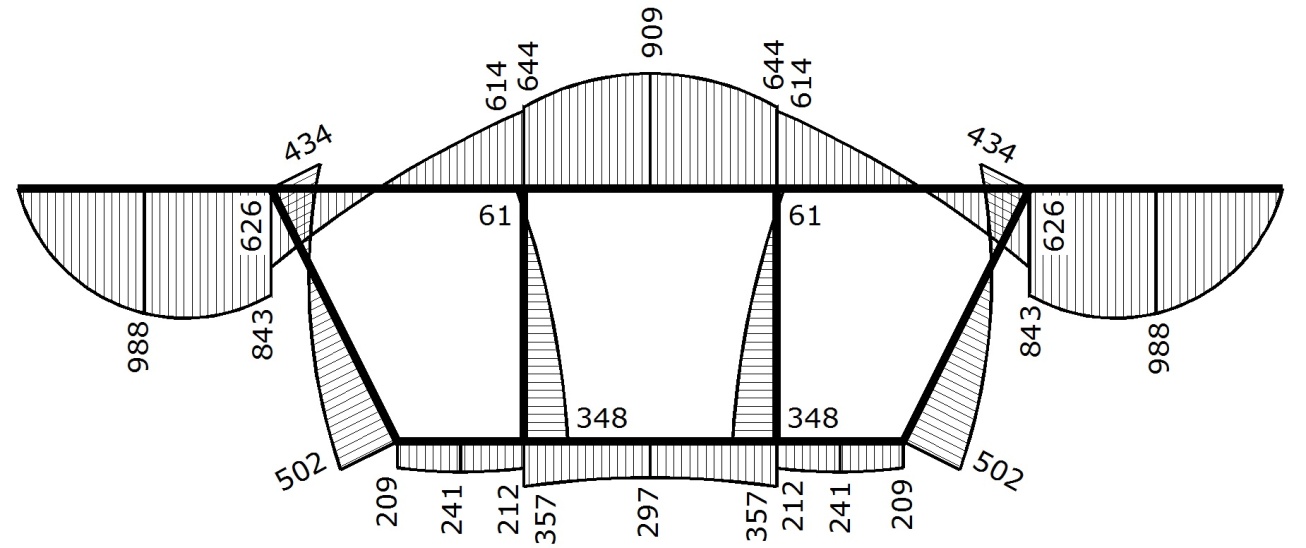
Эпюра касательных напряжений, отнесенных к моменту стесненного кручения,  τ_ω/M_ω×10⁷, 1/см³

 

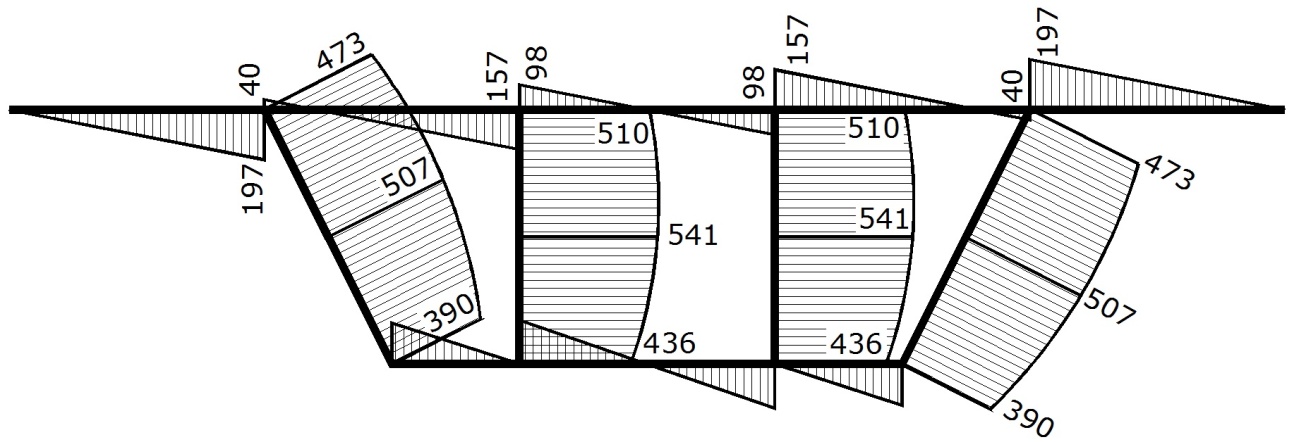
Эпюра касательных напряжений, отнесенных к поперечной силе,  τ_u/Q_u×10⁵, 1/см²

 

Результаты решения в Тонус:

 

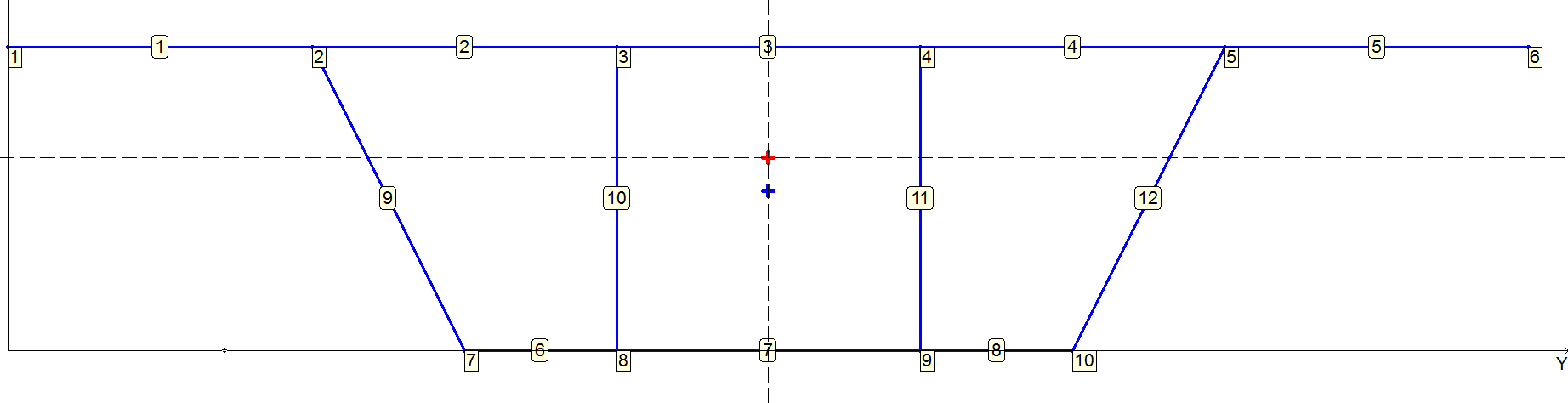
Нумерация вершин и полос, положение центра масс и центра изгиба

 

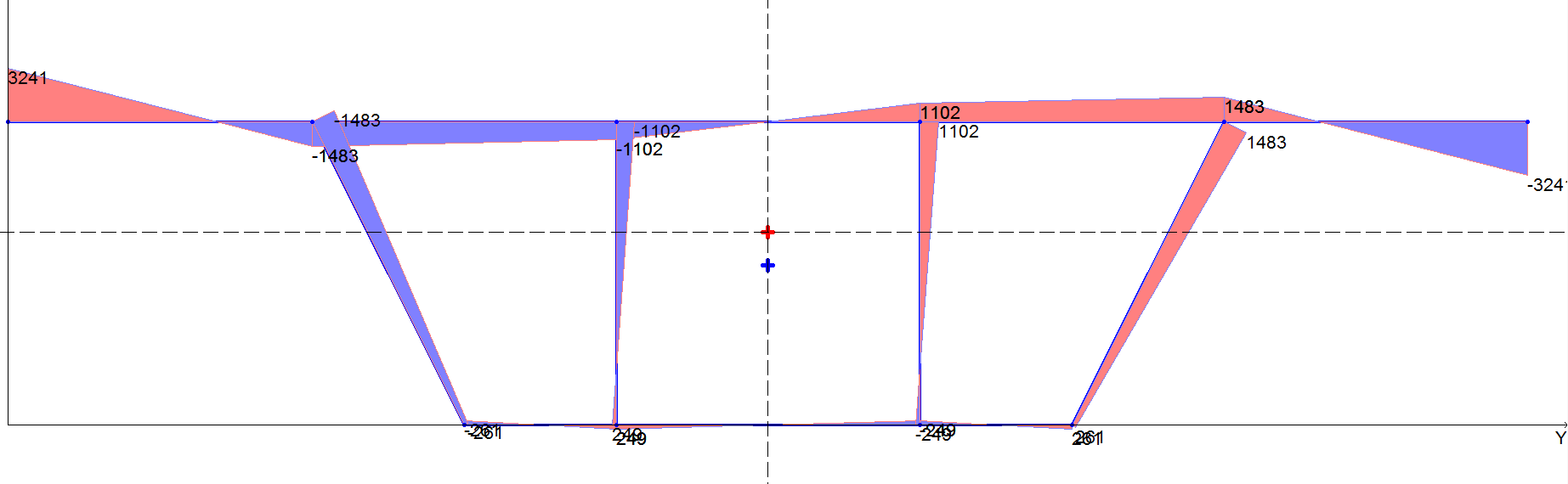
Эпюры секториальных площадей ω, см²

 

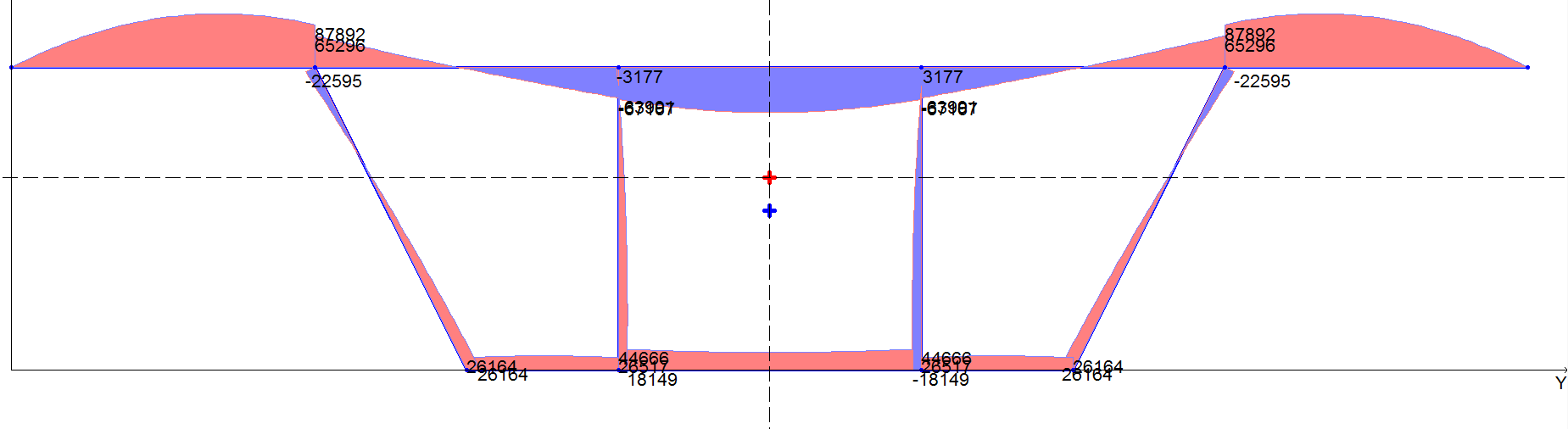
Эпюра секториального статического момента S_ω, см⁴

 

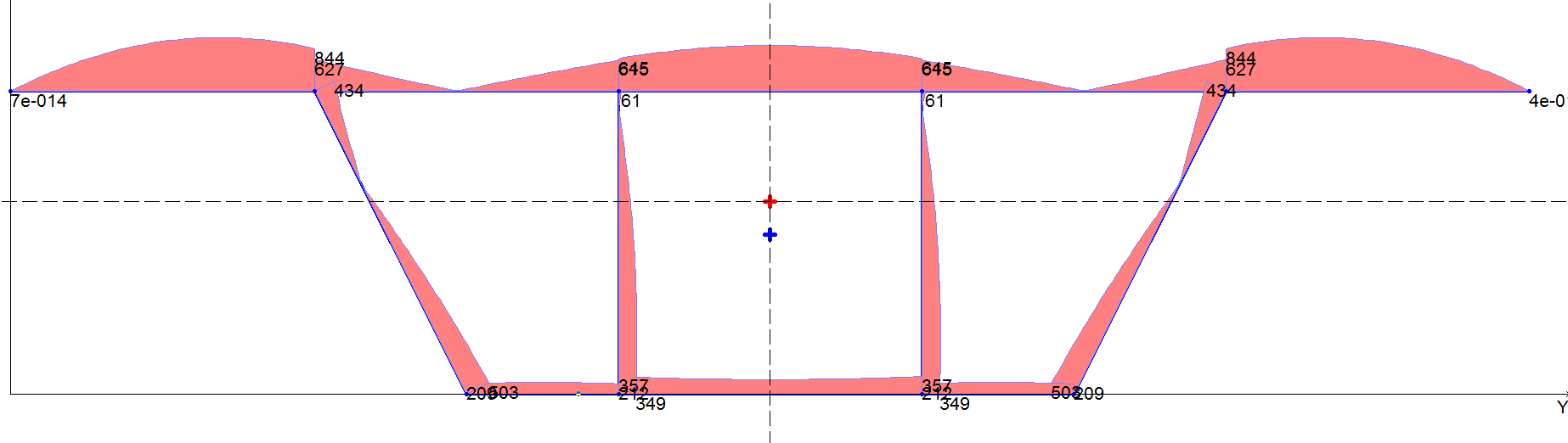
Эпюра модуля касательных напряжений τ_ω для значения момента стесненного кручения M_ω = 10⁷, кНсм

 

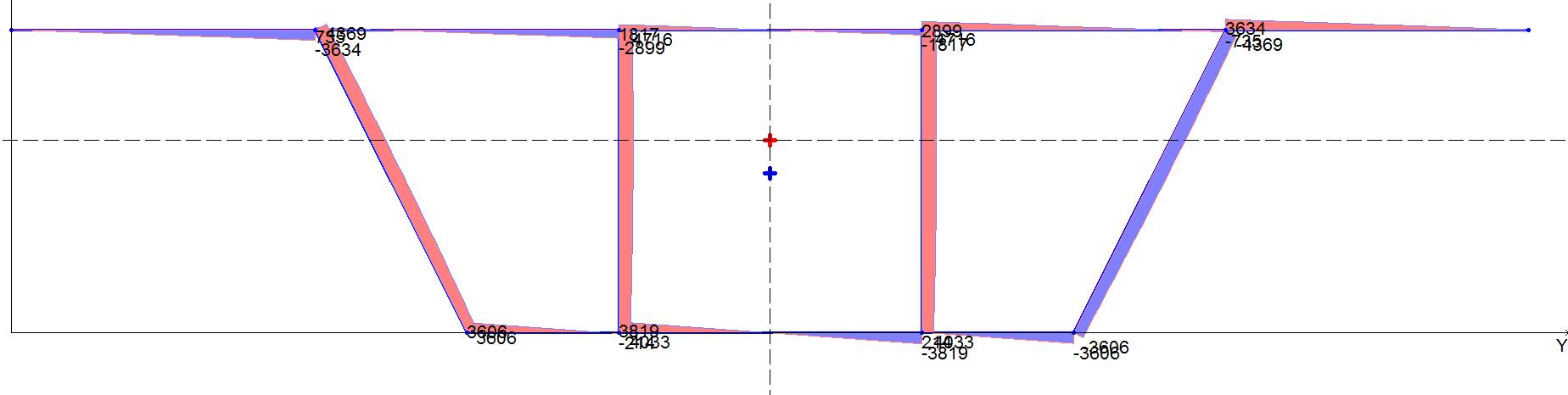
Эпюра статического момента S_v, см³

 

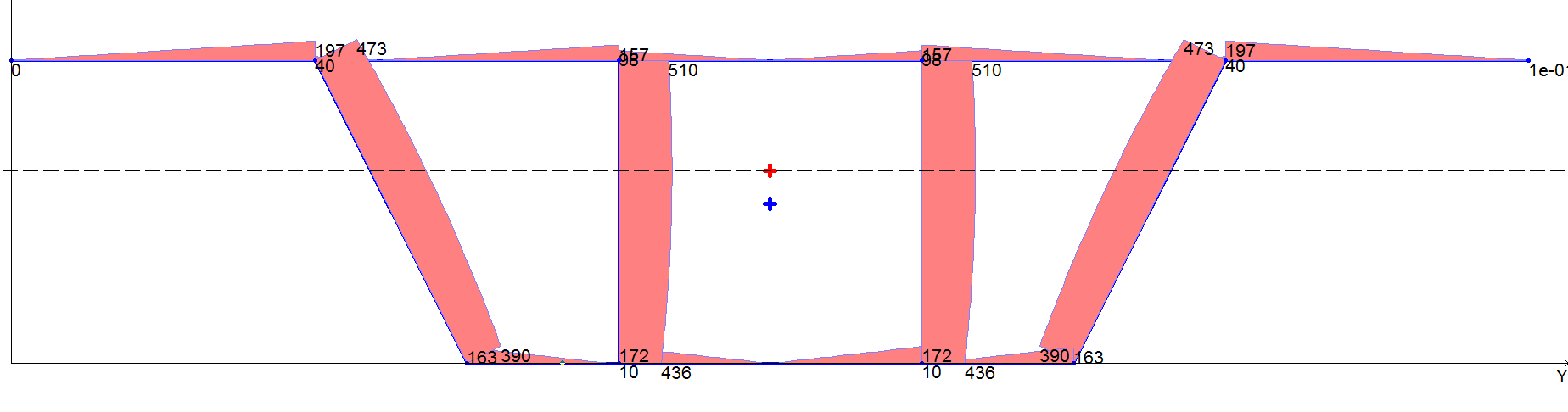
Эпюра модуля касательных напряжений τu для значения поперечной силы Q_u = 10⁵, кН

 

 

Сравнение решений:

Номер элемента	Номер вершины	Статический секториальный момент Sω, см4			Статический момент Sv, см3
		Источник*	ТОНУС	Отклонение, %	Источник**	ТОНУС	Отклонение, %
1	1	0	0	0	0	0	0
1	2	87776	87892	0,13	3643	3634	0,25
2	2	65181	65296	0,18	740	741	0,14
2	3	63932	64036	0,16	2903	2899	0,14
3	3	67055	67159	0,16	1812	1817	0,28
6	7	26114	26164	0,19	3595	3606	0,3
6	8	26489	26517	0,11	–	10	–
7	8	44606	44666	0,13	3816	3819	0,08
9	2	22595	22595	0	4373	4369	0,09
9	7	26135	26164	0,11	3606	3606	0
10	3	3176	3177	0,03	4715	4716	0,02
10	8	18117	18149	0,15	4031	4033	0,05
Примечания: *Значение статического секториального момента Sω рассчитывалось с использованием значения τω/Mω, полученного из источника, как (Iω = 1041229484 см6): Sω = τωIωt / Mω; ** Значение статического момента Sv рассчитывалось с использованием значения τu/Qu, полученного из источника, как (Iv = 1849016 см4): Sv = τuIvt / Qu .

 

Номер элемента	Номер вершины	Касательное напряжение τω, кН/см2 (при Mω = 107, кНсм)			Касательное напряжение τu, кН/см2 (при Qu = 105, кН)
		Источник	ТОНУС	Отклонение, %	Источник	ТОНУС	Отклонение, %
1	1	0	0	0	0	0	0
1	2	843	844	0,12	197	197	0
2	2	626	627	0,16	40	40	0
2	3	614	615	0,16	157	157	0
3	3	644	645	0,16	98	98	0
6	7	209	209	0	162	163	0,6
6	8	212	212	0	–	10	0
7	8	357	357	0	172	172	0
9	2	434	434	0	473	473	0
9	7	502	503	0,20	390	390	0
10	3	61	61	0	510	510	0
10	8	348	349	0,29	436	436	0

 

Номер вершины	Секториальная площадь, см2
	Источник	ТОНУС	Отклонение, %
1	+3241	+3241	0
2	–1483	–1483	0
3	–1102	–1102	0
7	–261	–261	0
8	+249	+249	0