Секториальные характеристики C-образного тонкостенного сечения

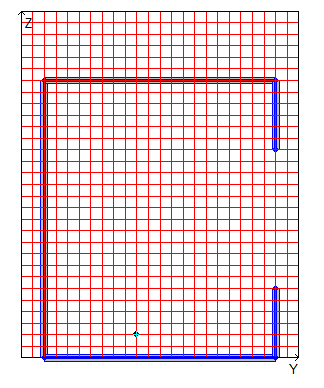
Цель: Проверка точности определения геометрических характеристик С-образного тонкостенного сечения.

Формулировка задачи: Для тонкостенного поперечного сечения стержня с С-образной формой проверить точность вычисления геометрических характеристик.

Ссылки: W.C.Young, R.G.Budynas, Roark's Formulas for Stress and Strain, New York , McGraw-Hill,  New York, 2002.

Исходные данные:

Геометрические размеры сечения:

b = 100 см,

b₁ = 30 см,

h = 120 см,

t = 3 см.

 

Файл с исходными данными: СSection.tns

 

 

Результаты решения в Тонус:

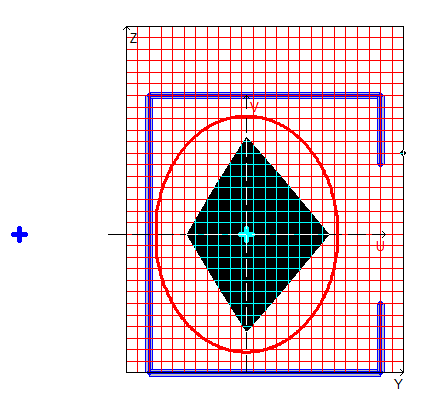
Расчетная модель, координатные и главные оси, центр масс, эллипс инерции, ядро сечения

Сравнение решений:

Параметр	Теория	ТОНУС	Отклонение, %
Площадь поперечного сечения, A см2	1140	1140	0
Условная площадь среза вдоль главной оси U, Av,y см2	600	600	0
Условная площадь среза вдоль главной оси V, Av,z см2	540	540	0
Момент инерции при свободном кручении, It см4	3420	3420	0
Секториальный момент инерции, Iw см6	8024714070,28	8024727272,72	0.00016
Координата центра изгиба по оси Y, yb см	-46,364	-46,364	0
Координата центра изгиба по оси Z, zb см	60	60	0

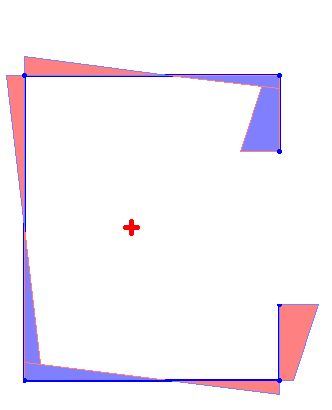
Эпюры секториальных площадей

Замечания: При аналитическом решении геометрические характеристики определяются по следующим формулам:

\[ A=(2b+2b_{1} +h)t; \] \[ A_{v,y} =2bt; \] \[ A_{v,z} =t(h+2b_{1} ); \] \[ I_{t} =\frac{t^{3}}{3}\left( {h+2b+2b_{1} } \right); \] \[ e=b\frac{3h^{2}b+6h^{2}b_{1} -8b_{1}^{3} }{h^{3}+6h^{2}b+6h^{2}b_{1} +8b_{1}^{3} -12hb_{1}^{2} }; \] \[ I_{\omega } =t\left[ {\frac{h^{2}b^{2}}{2}\left( {b_{1} +\frac{b}{3}-e-\frac{2eb_{1} }{b}+\frac{2b_{1}^{2} }{h}} \right)+\frac{h^{2}e^{2}}{2}\left( {b+b_{1} +\frac{h}{6}-\frac{2b_{1}^{2} }{h}} \right)+\frac{2b_{1}^{3} }{3}(b+e)^{2}} \right]. \]