Секториальные характеристики тонкостеннного сектора кольца

Цель: Проверка точности определения геометрических характеристик тонкостенного сектора кольца.

Формулировка задачи: Для тонкостенного поперечного сечения стержня с формой сектора кольца проверить точность вычисления геометрических характеристик.

Ссылки: W.C. Young, R.G. Budynas, Roark's Formulas for Stress and Strain, New York , McGraw-Hill, New York, 2002.

Исходные данные:

Геометрические размеры сечения:

r = 100 см,

t = 3 см,

α= 67,5°.

Расчетная модель: Расчетная модель образуется на основе модели срединного контура. Модель контура представляет собой многоугольник, вписанный в дугу окружности с заданными характеристиками. Количество вершин многоугольника в модели – 24.

Файл с исходными данными: ArcSection.tns

Результаты решения в Тонус:

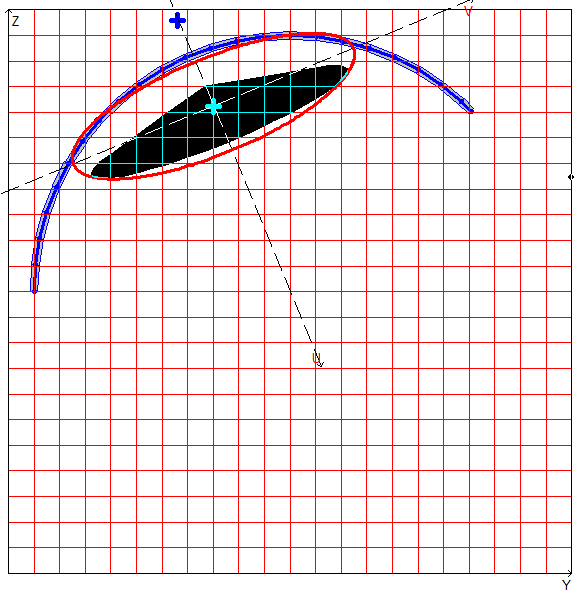
Расчетная модель, координатные и главные оси, центр масс, эллипс инерции, ядро сечения

Сравнение решений:

Параметр	Теория	ТОНУС	Отклонение, %
Площадь поперечного сечения, A см²	706,858	707,159	0,043
Условная площадь среза вдоль главной оси U, A_v,y см²	247,313	247,879	0,229
Условная площадь среза вдоль главной оси V, A_v,z см²	459,487	459,279	0,045
Момент инерции при свободном кручении, I_t см⁴	2126,858	2121,476	0,253
Секториальный момент инерции, I_w см⁶	135771063,361	136173663,259	0,297
Координата центра изгиба по оси Y, y_b см	66,229	66,232	0,005
Координата центра изгиба по оси Z, z_b см	215,963	215,981	0,008

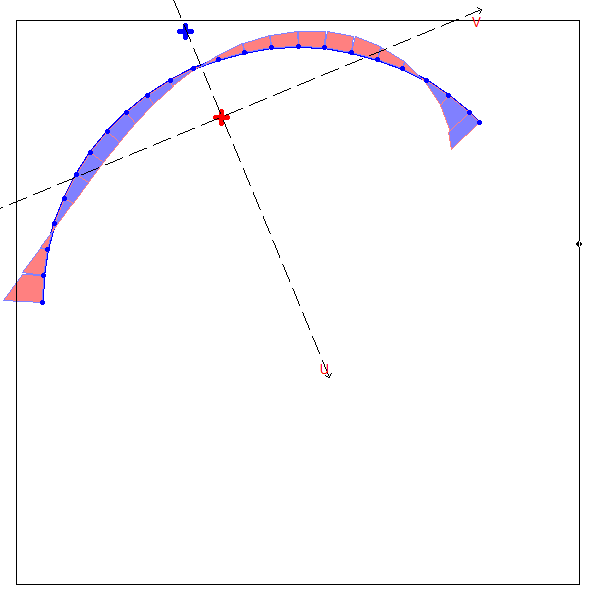
Эпюры секториальных площадей

Замечания: При аналитическом решении геометрические характеристики определяются по следующим формулам:

\[ A=r\alpha ; \] \[ A_{v,y} =2rt\left( {\frac{\alpha }{2}-\frac{\sin (2\alpha )}{4}} \right); \] \[ A_{v,z} =2rt\left( {\frac{\alpha }{2}+\frac{\sin (2\alpha )}{4}} \right); \] \[ I_{t} =\frac{2}{3}t^{3}r\alpha ; \] \[ I_{\omega } =\frac{2tr^{5}}{3}\left[ {\alpha^{3}-6\frac{(\sin \alpha -\alpha \cos \alpha )^{2}}{\alpha -\sin \alpha \cos \alpha }} \right]; \] \[ e=2r\frac{\sin \alpha -\alpha \cos \alpha }{\alpha -\sin \alpha \cos \alpha }. \]