Секториальные площади, статические моменты и касательные напряжения для тонкостенного открытого сечения
Цель: Проверка точности определения секториальных площадей ω, секториального статического момента Sω, а также касательных напряжений τω, обусловленных стесненным кручением для тонкостенного окрытого сечения.
Имя файла с исходными данными: Prokic_open.tns
Формулировка задачи: Для тонкостенного открытого поперечного сечения проверить точность вычисления секториальных площадей, статических моментов и касательных напряжений.
Ссылки: Prokić A. Computer program for determination of geometrical properties of thin-walled beams with open-closed section // Computers and Structures, Vol. 74 (2000). – pp. 705 – 715.
Исходные данные:
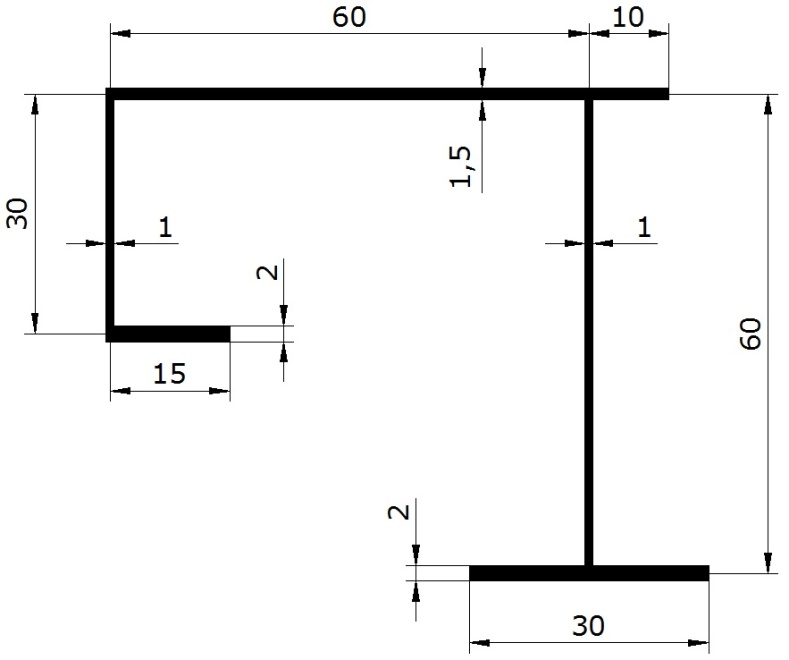
Открытое тонкостенное сечение с размерами, см
Результаты решения из источника:
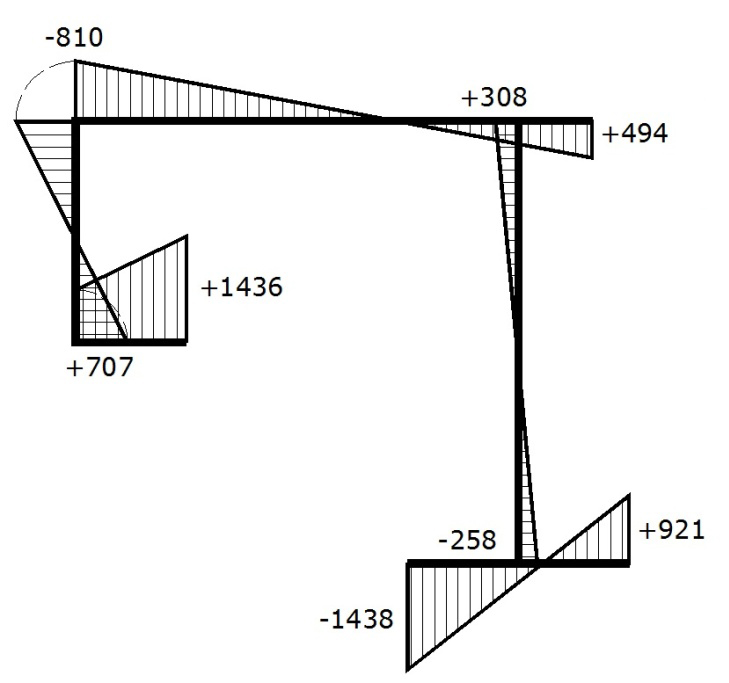 |
 |
|
Эпюра секториальных площадей ω, см2
|
Эпюра касательных напряжений, отнесенных к моменту стесненного кручения, |
Результаты решения в Тонус:
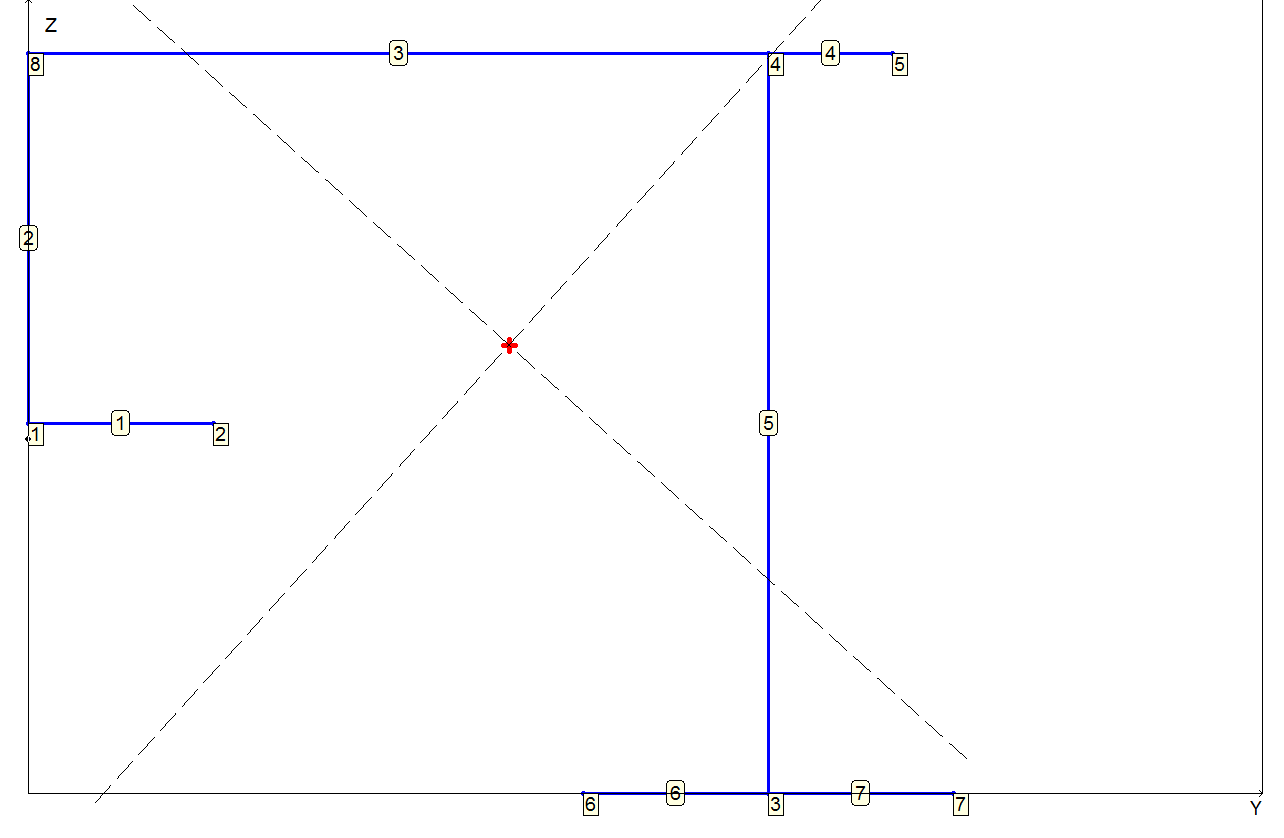
Нумерация вершин и полос, положение центра масс и центра изгиба
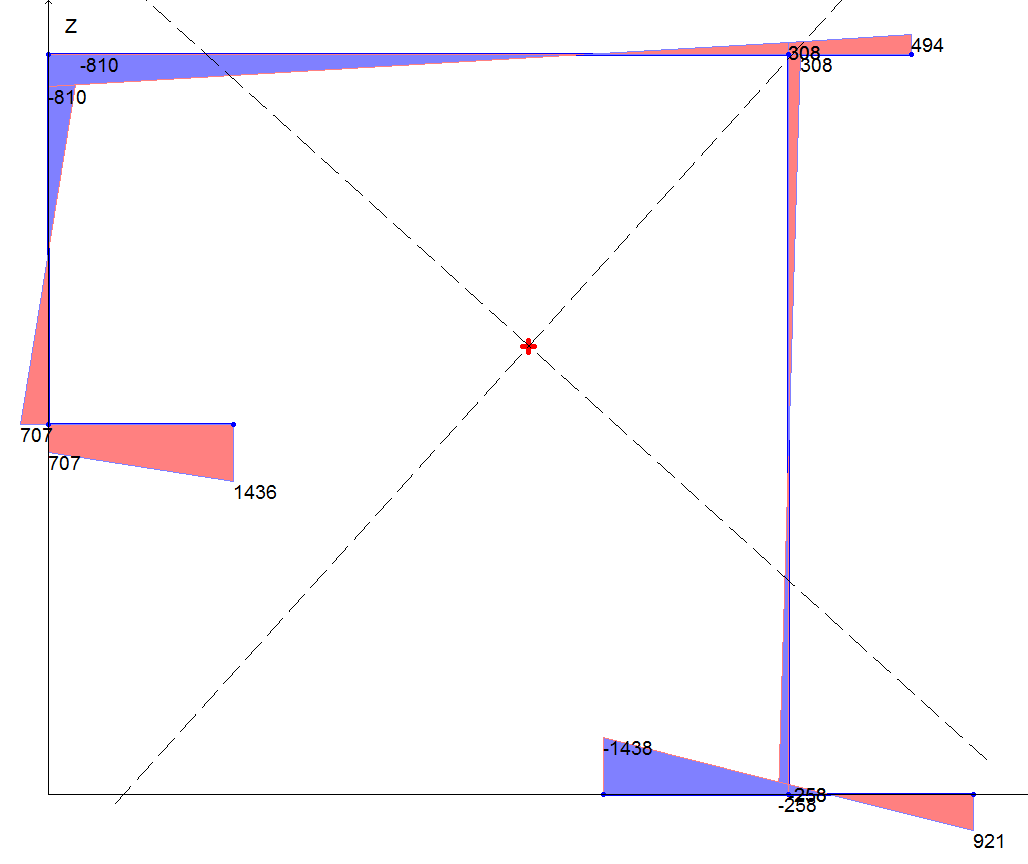
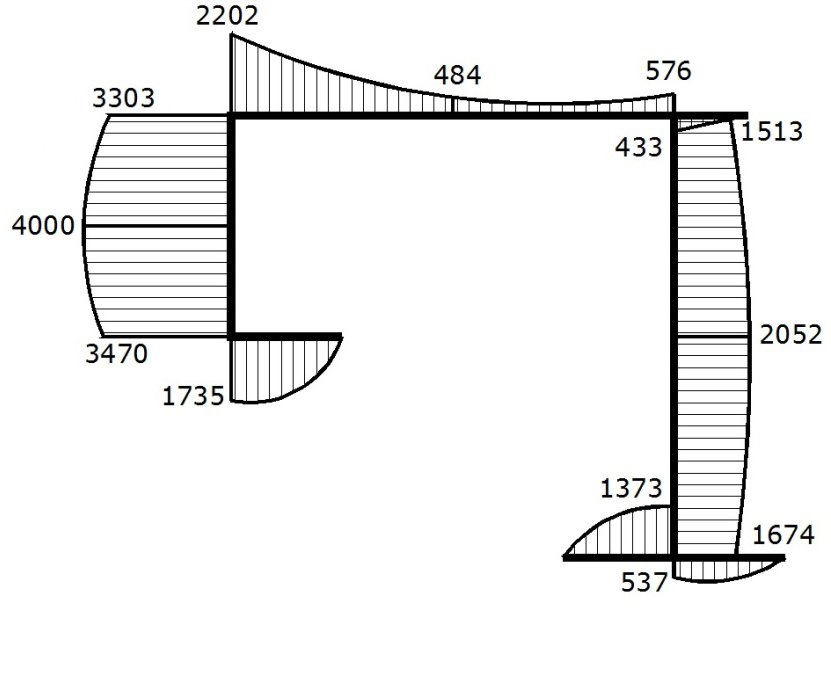
Эпюра секториальных площадей ω, см2
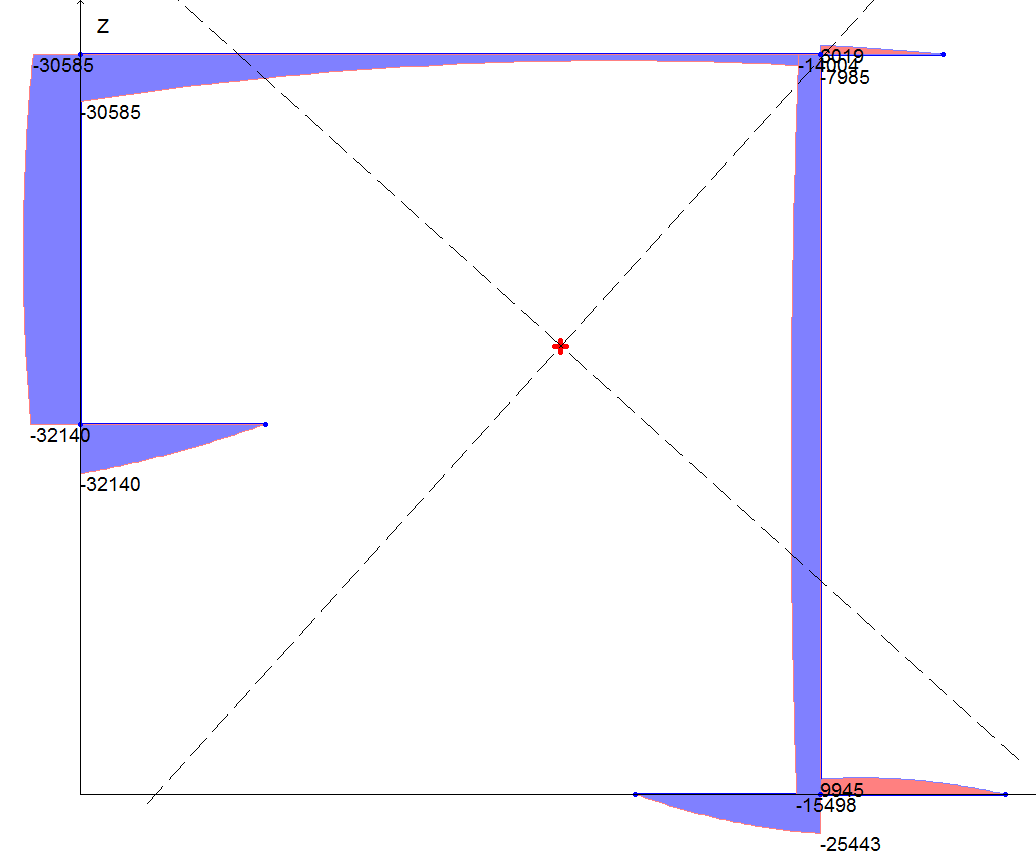
Эпюра секториального статического момента Sω, см4
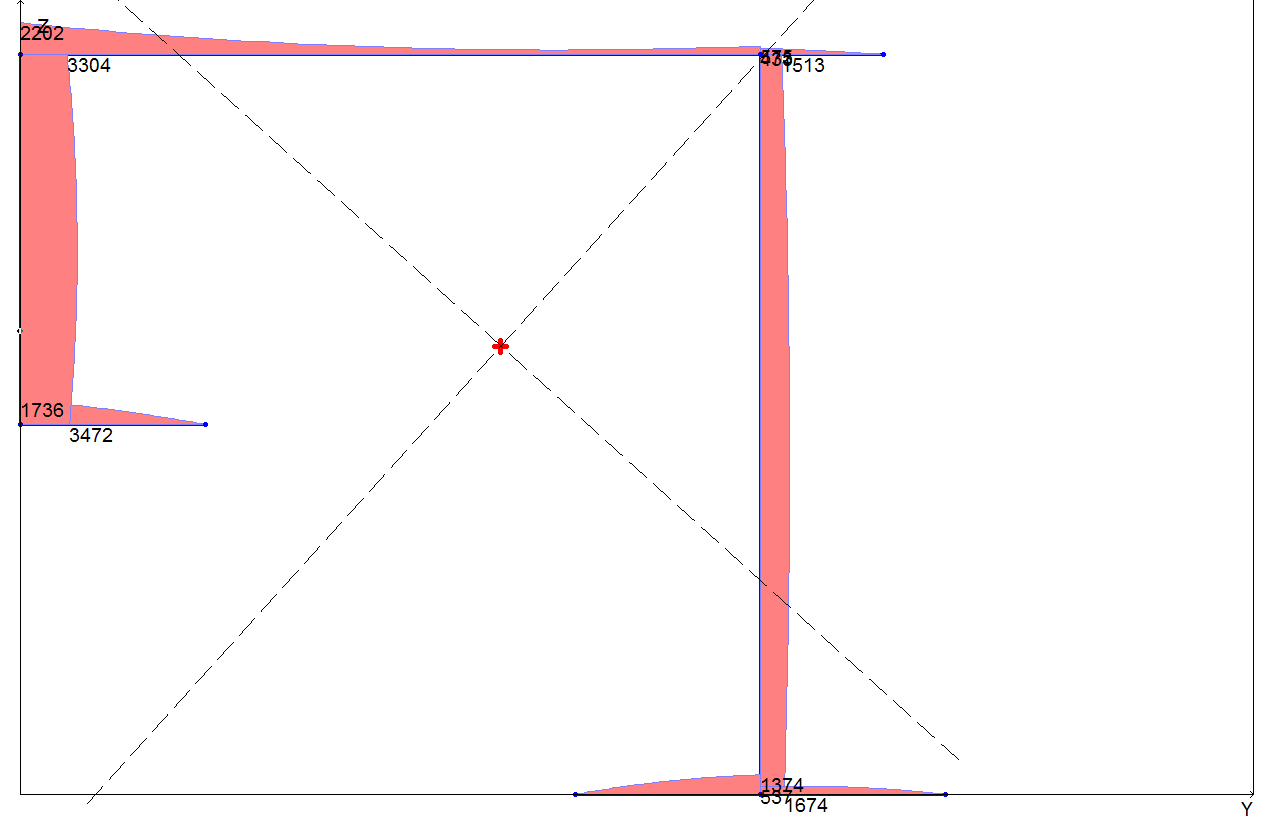
Эпюра модуля касательных напряжений τω для значения момента стесненного кручения Mω = 107, кНсм
Сравнение решений:
|
Номер элемента |
Номер вершины |
Статический секториальный момент, см4 |
Касательное напряжение, кН/см2 (при Mω = 107, кНсм) |
||||
|---|---|---|---|---|---|---|---|
|
Источник* |
ТОНУС |
Отклонение, % |
Источник |
ТОНУС |
Отклонение, % |
||
|
1 |
1 |
32126 |
32140 |
0,04 |
1735 |
1736 |
0,06 |
|
1 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
1 |
32126 |
32140 |
0,04 |
3470 |
3472 |
0,06 |
|
2 |
8 |
30580 |
30585 |
0,02 |
3303 |
3304 |
0,06 |
|
3 |
8 |
30580 |
30585 |
0,02 |
2202 |
2202 |
0 |
|
3 |
4 |
7999 |
7985 |
0,18 |
576 |
575 |
0,17 |
|
4 |
4 |
6013 |
6019 |
0,1 |
433 |
432 |
0,23 |
|
4 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
4 |
14008 |
14004 |
0,03 |
1513 |
1513 |
0 |
|
5 |
3 |
15498 |
15498 |
0 |
1674 |
1674 |
0 |
|
6 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
|
6 |
3 |
25423 |
25443 |
0,08 |
1373 |
1374 |
0,07 |
|
7 |
3 |
9943 |
9945 |
0,02 |
537 |
537 |
0 |
|
7 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Примечание: *Значение статического секториального момента Sω рассчитывалось с использованием значения τω/Mω, полученного из источника, как (Iω = 92582119 см6): Sω.= τωIωt / Mω. |
|||||||
|
Номер вершины |
Секториальная площадь, см2 |
||
|---|---|---|---|
|
Источник |
ТОНУС |
Отклонение, % |
|
|
1 |
707 |
707 |
0 |
|
2 |
1436 |
1436 |
0 |
|
3 |
-258 |
-258 |
0 |
|
4 |
308 |
308 |
0 |
|
5 |
494 |
494 |
0 |
|
6 |
-1438 |
-1438 |
0 |
|
7 |
921 |
921 |
0 |
|
8 |
-810 |
-810 |
0 |