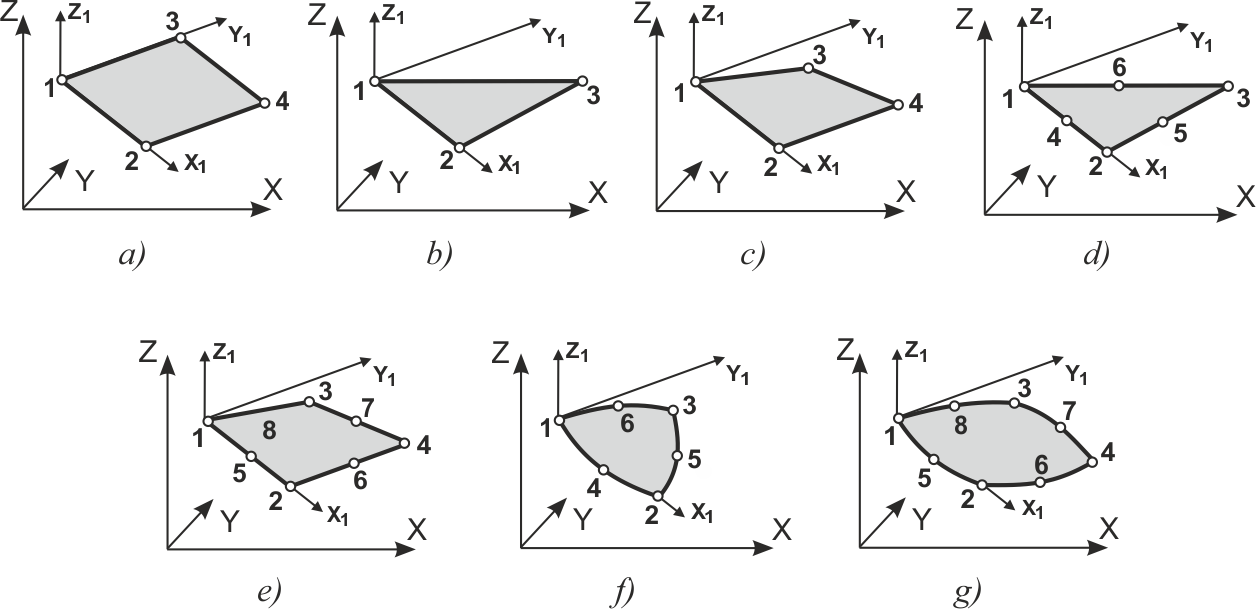
В систему SCAD включены различные плоские конечные элементы, имеющие форму треугольника и четырехугольника. Число узлов в некоторых типах элементов может быть больше чем число вершин. В этом случае дополнительные узлы лежат на одной или нескольких сторонах элемента и их номера следуют после номеров вершин в произвольном порядке.
Эти КЭ всегда расположены в плоскости XOY и в их узлах определено по три степени свободы: W — вертикальное перемещение (прогиб), а также UX, UY — углы поворота относительно осей X и Y. КЭ могут использоваться в схемах с признаками 3, 5, 8 и 9 и иметь изотропный, ортотропный или анизотропный материал. Вычисляются моменты MX, MY, MXY и перерезывающие силы QX и QY. При задании коэффициента упругого основания С1 вычисляется RZ.

Рис. 1. Конечные элементы плиты
Перечень КЭ для расчета тонких изгибаемых пластин приведен в таблице 1.
Таблица 1
Тип |
Наименование |
Число узлов |
Порядок нумерации узлов и местные оси |
Коментарии |
|---|---|---|---|---|
11 |
Прямоугольный |
4 |
рис.1, а |
полусовместный [18,22,23] |
12, 14 |
Треугольный |
3 |
рис.1, б |
несовместный [18,22,23] |
13 |
Прямоугольный |
4 |
рис.1, а |
несовместный [28] |
15 |
Треугольный |
3-6 |
рис.1, г |
|
16 |
Четырехугольный |
4-8 |
рис.1, д |
SubAreas, вариант 2 [25,23] |
18 |
Треугольный |
3-6 |
рис.1, г |
SubAreas, вариант 2 [24,23] |
19 |
Четырехугольный |
4 |
рис.1, в |
SubAreas, [25,23] |
20 |
Четырехугольный |
4-8 |
рис.1, д |
SubAreas, [24,22], вариант 1 |
[1] SubAreas – метод подобластей: треугольные и четырехугольные элементы разбиваются, соответственно, медианами и диагоналями на треугольники, на каждом из которых используются для аппроксимации полиномы соответствующей степени таким образом, чтобы обеспечивалась совместность. Получаем кусочно-полиномиальные аппроксимации.
Данные элементы предназначены для расчета плит средней толщины и реализуют теорию Рейсснера-Миндлина. Они полностью аналогичны элементам для расчета тонких плит с точки зрения задания исходных данных. Отличие их от элементов, приведенных в табл. 1, только в номере типа — он на 100 больше. Например, элемент 120 — четырехугольный элемент с числом узлов от 4-х до 8-ми, как и элемент 20.
В каждом узле элементов вводится по три степени свободы: w — вертикальное перемещение (прогиб), положительное направление совпадает с направлением оси Z, а также UX и UY углы поворота относительно осей X и Y.
Таблица 2. Типы элементов для расчета плит средней толщины(теория Рейсснера-Миндлина)
Тип |
Наименование |
Число узлов |
Порядок нумерации узлов и местные оси |
Коментарии |
|---|---|---|---|---|
111 |
Прямоугольный |
4 |
рис. а |
|
112 |
Треугольный |
3 |
рис. б |
JIDR3 [91,23] |
115 |
Треугольный |
3-6 |
рис. г |
JIDR3-6 [91,23] |
116 |
Четырехугольный |
4-8 |
рис. ж |
изопараметрический, JIDR [91,23] |
118 |
Треугольный |
3-6 |
рис. е |
изопараметрический, JIDR [91,23] |
119 |
Четырехугольный |
4 |
рис. б |
JIDR [91,23] |
120 |
Четырехугольный |
4-8 |
рис. д |
JIDR, SubAreas [91,23] |
512 |
Треугольный |
3 |
рис. б |
|
517 |
Четырехугольный |
4 |
рис. в |
|
518 |
Треугольный |
3 |
рис. б |
DSG3 [76] |
Перечень КЭ для расчета пластин по теории Рейсснера-Миндлина приведен в таблице 2.
[2] JIDR, joint interpolation of displacements and rotations (Совместная интерполяция перемещений и углов поворота) [91,23].
[3] DSG, Discrete Shear Gap [76].
[4] MITC, Mixed Interpolation of Tensorial Components [3,75].
Все рассматриваемые в этом разделе элементы позволяют рассчитывать как плосконапряженные, так и плоскодеформируемые системы (по признаку, который задается при описании жесткостных характеристик элементов).
Существуют следующие группы типов элементов:
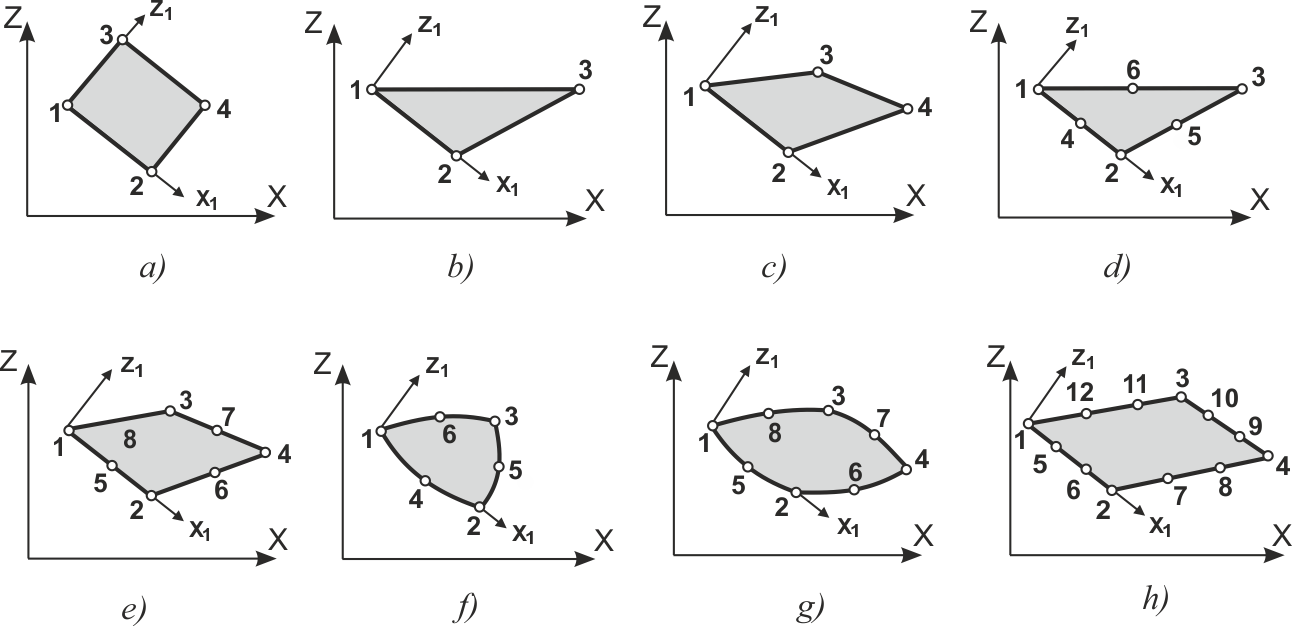
Рис. 2. Плоские конечные элементы
Таблица 3. Типы элементов для плоской задачи теории упругости
Степени свободы узлов |
Тип |
Наименование |
Число узлов |
Порядок нумерации узлов и местные оси |
Коментарии |
|---|---|---|---|---|---|
X, Z |
21 |
Прямоугольный |
4 |
рис. а |
полилинейные функции формы |
22 |
Треугольный |
3 |
рис. б |
линейные функции формы |
|
25 |
Треугольный |
3-6 |
рис. г |
SubAreas [16, 23] |
|
29 |
Четырехугольный |
4-12 |
рис. з |
SubAreas [26, 23] |
|
30 |
Четырехугольный |
4-8 |
рис. д |
SubAreas [26, 23] |
|
X, Y, Z |
23 |
Прямоугольный |
4 |
рис. а |
полилинейные функции формы |
24 |
Треугольный |
3 |
рис. б |
линейные функции формы |
|
26 |
Четырехугольный |
4-8 |
рис. ж |
изопараметрический |
|
27 |
Четырехугольный |
4-8 |
рис. д |
SubAreas [26, 23] |
|
28 |
Треугольный |
3-6 |
рис. е |
изопараметрический |
|
Элементы с вращательными (DDF) и квазивращательными степенями свободы (QRDF) |
|||||
X, Y, UY |
121 |
Прямоугольный |
4 |
рис. а |
|
122 |
Треугольный |
3 |
рис. б |
DDF, несовместный [90, 23] |
|
125 |
Треугольный |
3-6 |
рис. г |
DDF, SubAreas [90, 23] |
|
129 |
Четырехугольный |
4-8 |
рис. д |
DDF, SubAreas, несовместный [90, 23] |
|
130 |
Четырехугольный |
4-8 |
рис. д |
DDF, SubAreas [90, 23] |
|
526 |
Четырехугольный |
4 |
рис. в |
||
527 |
Четырехугольный |
4 |
рис. в |
QRDF, SubAreas [90, 23] |
|
528 |
Треугольный |
3 |
рис. б |
QRDF [90, 23] |
|
[6] DDF – Drilling degrees of freedom (с вращательными степенями свободы) [23]
[7] QRDF – Quasi-rotational degrees of freedom (с квазивращательными степенями свободы) [23]
Все элементы могут иметь изотропный, ортотропный или анизотропный материал, а также трансверсально-изотропный для плоской деформации.
Перечень элементов и их основные свойства приведены в таблице 3.
Вычисляемые напряжения — NX, NZ, NXZ, а также NY — при расчете конструкций, находящихся в состоянии плоской деформации.
При задании коэффициента упругого основания Сuv вычисляются Rx и Rz.
Конечные элементы, предназначенные для расчета тонких пологих оболочек, могут занимать любое положение в пространстве. В узлах элементов определено по шесть степеней свободы — U, V, W, UX, UY и UZ (три линейных перемещения вдоль и три угла поворота вокруг координатных осей). Степени свободы U, V отвечают мембранным, а W, UX, UY — изгибным деформациям.
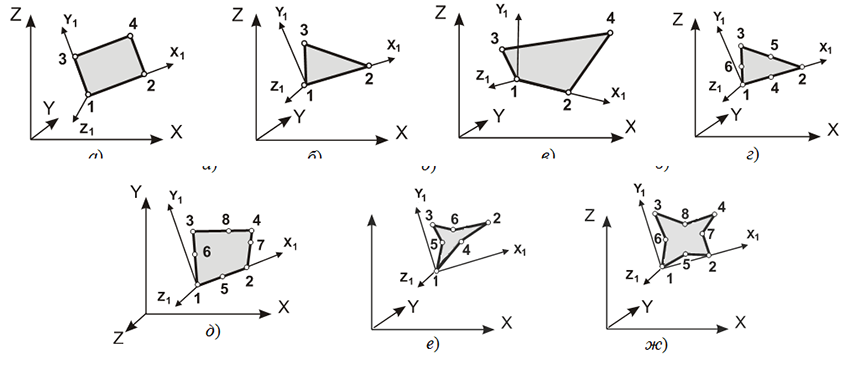
Рис. 3. Элементы оболочки
Существуют следующие группы типов элементов:
Материал — изотропный, ортотропный и анизотропный.
Перечень элементов приведен в таблице 4.
Таблица 4. Элементы для расчета тонких оболочек (теория Киргхофа-Лява)
Тип |
Наименование |
Число узлов |
Порядок нумерации узлов и местные оси |
Степени свободы |
Коментарии |
|---|---|---|---|---|---|
41 |
Прямоугольный |
4 |
рис. а |
U, V |
полилинейные функции формы |
W, UX, UY |
полусовместный [18, 22, 23] |
||||
42 |
Треугольный |
3 |
рис. б |
U, V |
линейные функции формы |
W, UX, UY |
несовместный [18, 22, 23] |
||||
43 |
Прямоугольный |
4 |
рис. а |
U, V |
полилинейные функции формы |
W, UX, UY |
несовместный [28, 23] |
||||
44 |
Четырехугольный |
4 |
рис. в |
U, V |
SubAreas [26, 23] |
W, UX, UY |
SubAreas [25, 23] |
||||
45 |
Треугольный |
3-6 |
рис. г |
U, V |
SubAreas [16, 23] |
W, UX, UY |
SubAreas [24, 23], вариант 1 |
||||
46 |
Четырехугольный |
4-8 |
рис. в |
U, V |
SubAreas [26, 23] |
W, UX, UY |
SubAreas, вариант 2 [25, 23] |
||||
48 |
Треугольный |
3-6 |
рис. г |
U, V |
SubAreas [16, 23] |
W, UX, UY |
SubAreas, вариант 2 [24, 23] |
||||
50 |
Четырехугольный |
4-8 |
рис. д |
U, V |
SubAreas [26, 23] |
W, UX, UY |
SubAreas, вариант 1 [25, 23] |
||||
Элементы с вращательными (DDF) и квазивращательными степенями свободы (QRDF) |
|||||
91 |
Прямоугольный |
4 |
рис. а |
U, V, UZ |
DDF, несовместный [90, 23] |
W, UX, UY |
полусовместный [18, 22, 23] |
||||
92 |
Треугольный |
3 |
рис. б |
U, V, UZ |
DDF, несовместный [90, 23] |
W, UX, UY |
несовместный [18, 22, 23] |
||||
93 |
Прямоугольный |
4 |
рис. а |
U, V, UZ |
DDF, несовместный [90, 23] |
W, UX, UY |
несовместный [28, 23] |
||||
94 |
Четырехугольный |
4 |
рис. д |
U, V, UZ |
DDF, SubAreas, несовместный [90, 23] |
W, UX, UY |
SubAreas, [25, 23] |
||||
95 |
Треугольный |
3-6 |
рис. г |
U, V, UZ |
DDF, SubAreas [90, 23] |
W, UX, UY |
SubAreas [24, 23] |
||||
96 |
Четырехугольный |
4-8 |
рис. д |
U, V, UZ |
DDF, SubAreas [90, 22] |
W, UX, UY |
SubAreas [25, 23] |
||||
97 |
Четырехугольный |
4-8 |
рис. д |
U, V, UZ |
DDF, SubAreas, несовместный [90, 23] |
W, UX, UY |
SubAreas [25, 23] |
||||
591 |
Прямоугольный |
4 |
рис. а |
U, V, UZ |
QRDF4 [90, 23] |
W, UX, UY |
полусовместный [18, 22, 23] |
||||
592 |
Треугольный |
3 |
рис. б |
U, V, UZ |
QRDF3 [90, 23] |
W, UX, UY |
несовместный [18, 22, 23] |
||||
593 |
Прямоугольный |
4 |
рис. в |
U, V, UZ |
QRDF4, [90, 23] |
W, UX, UY |
несовместный [28, 23] |
||||
594 |
Четырехугольный |
4 |
рис. в |
U, V, UZ |
QRDF4, SubAreas [23] |
W, UX, UY |
SubAreas [25, 23] |
||||
Вычисляются напряжения NX, NY, NXY, моменты MX, MY, MXY и перерезывающие силы QX и QY. При задании коэффициента упругого основания С1 вычисляется Rz, а при задании – Сuv вычисляются Rx и Ry.
Вграфическом постпроцесоре вычисляются усилия в сечении пластины SNX, SNZZ, SNXZ.
Данные элементы предназначены для расчета пологих оболочек с учетом сдвига и реализуют теорию Рейсснера-Миндлина. Они полностью аналогичны элементам для расчета тонких оболочек с точки зрения задания исходных данных.
Перечень элементов приведен в таблице 5.
Таблица 5. Элементы для расчета оболочек средней толщины (теория Рейсснера-Миндлина)
Тип |
Наименование |
Число узлов |
Порядок нумерации узлов и местные оси |
Степени свободы |
Коментарии |
|---|---|---|---|---|---|
141 |
Прямоугольный |
4 |
рис. а |
U, V |
полилинейные формы |
W, UX, UY |
JIDR, несовместный [91, 23] |
||||
142 |
Треугольный |
3 |
рис. б |
U, V |
линейные функции формы |
W, UX, UY |
JIDR3 [91, 23] |
||||
143 |
Четырехугольный изопараметрич. |
4 |
рис. в |
U, V |
полилинейные функции формы |
W, UX, UY |
MITC4, изопараметрический [3, 75, 23] |
||||
144 |
Четырехугольный |
4 |
рис. в |
U, V |
SubAreas [26, 23] |
W, UX, UY |
JIDR4, SubAreas [91, 23] |
||||
145 |
Треугольный |
3-6 |
рис. г |
U, V |
SubAreas [26, 23] |
W, UX, UY |
JIDR, SubAreas [91, 23] |
||||
146 |
Четырехугольный изопараметрич. |
4-8 |
рис. д |
U, V |
изопараметрический |
W, UX, UY |
JIDR, изопараметрический [91, 23] |
||||
147 |
Треугольный, изопараметрич. |
3-6 |
рис. е |
U, V |
изопараметрический |
W, UX, UY |
JIDR, изопараметрический [91, 23] |
||||
148 |
Треугольный
|
3 |
рис. б |
U, V |
линейные функции формы |
W, UX, UY |
DSG3M [23] |
||||
149 |
треугольный
|
3 |
рис. б |
U, V |
линейные функции формы |
W, UX, UY |
DSG3 [76, 23] |
||||
150 |
четырехугольный |
4-8 |
рис. д |
U, V |
JIDR, SubAreas [26, 23] |
W, UX, UY |
JIDR, SubAreas [91, 23] |
||||
Элементы с вращательными (DDF) и квазивращательными степенями свободы (QRDF) |
|||||
191 |
Прямоугольный |
4 |
рис. а |
U, V, UZ |
DDF, несовместный [90, 23] |
W, UX, UY |
JIDR [91, 23] |
||||
192 |
Треугольный |
3 |
рис. б |
U, V, UZ |
DDF, SubAreas, [90, 23] |
W, UX, UY |
JIDR, SubAreas [91, 23] |
||||
194 |
Четырехугольный |
4 |
рис. в |
U, V, UZ |
DDF, SubAreas [90, 23] |
W, UX, UY |
JIDR, SubAreas [91, 23] |
||||
195 |
Треугольный |
3-6 |
рис. г |
U, V, UZ |
DDF, SubAreas [91, 23] |
W, UX, UY |
JIDR, SubAreas [91, 23] |
||||
196 |
Четырехугольный |
4-8 |
рис. д |
U, V, UZ |
DDF, SubAreas [90, 23] |
W, UX, UY |
JIDR, SubAreas, [91, 23] |
||||
197 |
Четырехугольный |
4-8 |
рис. д |
U, V, UZ |
DDF, несовместный, SubAreas [90, 23] |
W, UX, UY |
JIDR, SubAreas, [91, 23] |
||||
542 |
Треугольный |
3 |
рис. б |
U, V, UZ |
QRDF [90, 23] |
W, UX, UY |
JIDR [91, 23] |
||||
543 |
Четырехугольный |
4 |
рис. в |
U, V, UZ |
QRDF, изопараметрический [90, 23] |
W, UX, UY |
MITC4, изопараметрический [3, 75, 23] |
||||
544 |
Четырехугольный |
4 |
рис. а |
U, V, UZ |
QRDF, SubAreas [90, 23] |
W, UX, UY |
JIDR, SubAreas [91, 23] |
||||
546 |
Четырехугольный |
4 |
рис. в |
U, V, UZ |
QRDF, изопараметрический [90, 23] |
W, UX, UY |
JIDR, изопараметрический [91, 23] |
||||
547 |
Трехугольный |
4 |
рис. б |
U, V, UZ |
QRDF [90, 23] |
W, UX, UY |
DSG3M [23] |
||||
548 |
Треугольный |
3 |
рис. б |
U, V, UZ |
QRDF [90, 23] |
W, UX, UY |
DSG3 [76, 23] |
||||