Общие сведения
Эти элементы предназначены для определения напpяженно-дефоpмиpованного
состояния тел вращения (осесимметричные твердые тела) из однородного
(по направлению любой из осей r, Z элемента) изотропного, тpансвеpсально-изотpопного
или ортотропного линейно-упpугого материала, находящихся под воздействием
осесимметричной нагрузки [30]. При осесимметричной
деформации напряженное состояние в любом сечении по оси симметрии тела
рассматривается как функция лишь радиуса r и высоты Z и определяется
двумя компонентами перемещений. Такие сечения показаны на рисунке. При
этом возможно рассмотрение одного из следующих случаев упругой симметрии:
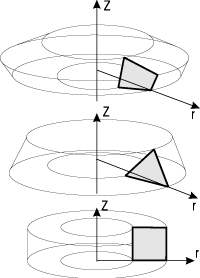
|
- полная симметрия (изотропное тело);
- плоскость изотропии (тpансвеpсально-изотpопное тело);
- три плоскости упругой симметрии (оpтотpопно-анизотpопное
или ортотропное тело).
Опишем их, используя следующие обозначения:
- εr, εz, εθ, γrz
— относительные линейные и угловая деформация;
- σr, σz, τrz — нормальные
и касательные напряжения в плоскости сечения;
- σθ — нормальное напряжение в направлении ортогональном
плоскости сечения;
- E, Ei — модули Юнга по главным направлениям
упругости;
- G — модуль сдвига;
- ν, νik — коэффициенты Пуассона, характеризующие
поперечное сокращение при сжатии или расширение при растяжении
в направлении осей координат. Первый индекс показывает направление
деформации, второй — направление действия силы.
|
Относительные линейные и угловая деформации εr, εz,
εθ, γrz через смещения запишутся следующим образом:
\[ \varepsilon_{z} =\frac{\partial \,v}{\partial \,z}, \quad \varepsilon_{r}
=\frac{\partial u}{\partial r}, \quad \varepsilon_{\theta } =\frac{u}{r},
\quad \gamma_{rz} =\frac{\partial u}{\partial z}+\frac{\partial v}{\partial
r}. \]
Деформации и напряжения связаны между собой зависимостями:
изотропное тело:
\[ \varepsilon_{z} =\frac{1}{E}\left[ {\sigma_{z} -\nu \left( {\sigma_{r}
+\sigma_{\theta } } \right)} \right], \] \[ \varepsilon_{r} =\frac{1}{E}\left[
{\sigma_{r} -\nu \left( {\sigma_{z} +\sigma_{\theta } } \right)} \right],
\] \[ \varepsilon_{\theta } =\frac{1}{E}\left[ {\sigma_{\theta } -\nu
\left( {\sigma_{z} +\sigma_{r} } \right)} \right], \] \[ \gamma_{rz} =\tau_{rz}
/G, \] \[ G=\frac{E}{2(1+\nu )}; \]
тpансвеpсально-изотpопное
тело:
\[ \varepsilon_{r} =\frac{1}{E}\sigma_{r} -\;\frac{\nu \,}{E}\sigma_{\theta
} -\;\frac{{\nu }'}{E_{z} }\,\sigma_{z} , \] \[ \varepsilon_{\theta }
=-\;\frac{\nu \,}{E}\sigma_{r} +\;\frac{1}{E}\sigma _{\theta } -\;\frac{{\nu
}'}{E_{z} }\sigma_{z} , \] \[ \varepsilon_{z} =-\;\frac{\;{{\nu }'}'}{E}\left(
{\sigma_{r} +\sigma _{\theta } } \right)+\;\frac{1}{E_{z} }\sigma_{z}
, \] \[ \gamma_{rz} =\tau_{rz} /G_{r} , \] \[ {\nu }'=\nu_{rz} =\nu_{\theta
\,z} ,\quad {{\nu }'}'=\nu_{zr} =\nu _{\,z\theta } \]
ортотропное тело:
\[ \varepsilon_{z} =\;\frac{1}{E_{z} }\sigma_{z} -\;\frac{\nu_{zr} }{E_{r}
}\sigma_{r} -\;\frac{\nu_{z\theta } }{E_{\theta } }\sigma_{\theta } ,
\] \[ \varepsilon_{r} =\frac{1}{E_{r} }\sigma_{r} -\;\frac{\nu_{r\theta
} }{E_{\theta } }\sigma_{\theta } -\;\,\frac{\nu_{rz} }{E_{z} }\sigma_{z}
, \] \[ \varepsilon_{\theta } =\;\frac{1}{E_{\theta } }\sigma_{\theta
} -\;\frac{\nu_{\theta \,r} }{E_{r} }\sigma_{r} -\,\;\frac{\nu_{\theta
\,z} }{E_{z} }\sigma_{z} , \] \[ \gamma_{rz} =\tau_{rz} /G \]
Предполагается, что выполнены условия симметрии: Erνrθ=
Eθνθr , Ezνzr=Errνrz ,
Eθνθz= Ezνzθ , являющиеся
обязательными для любого анизотропного материала, для которого справедливо
допущение о существовании упругого потенциала.
