Строительные нормы и анализ устойчивости стержней
В комплексе SCAD момент потери
устойчивости определяется для строго
прямолинейного, идеально упругого стержня. При этом может оказаться,
что некоторый стержень перенапряжен и уже потерял устойчивость при нагрузке,
например, 80% от действующей.
Формулы норм предусматривают упругопластическую
работу стержня с начальными несовершенствами (именно таким образом
построена кривая коэффициентов продольного изгиба φ(\( \overline{\lambda}
\)), приведенная в них). Согласно нормам может оказаться, что тот же стержень
тоже перенапряжен и потерял несущую способность при нагрузке, например,
76% от действующей. В этом случае 76% не очень сильно отличается от 80%.
Но в других случаях разница может быть очень большой. Для объяснения этого
явления можно воспользоваться примерной схемой, показанной на рисунке.
Схемы такого типа можно найти в учебниках и справочниках по стальным конструкциям
(см., например, или ).
Из приведенных на рисунке графиков видно, что при малых гибкостях значения
φ существенно различаются. Эту разницу можно увидеть, сравнив результаты,
полученные с помощью программы Кристалл,
которая реализует нижнюю кривую из рисунка (согласно рекомендациям норм),
и комплекса SCAD, где реализовано
классическое решение Эйлера, которое дается формулой (2)
при наличии шарниров на концах стержня.
В качестве примера рассмотрим расчетную модель, составленную из четырех
стержневых конечных элементов кольцевого сечения. Критическая нагрузка
такой сжатой стойки получается на 44% больше, чем это следует, например,
из формулы 7 СНиП II-23-81*, поскольку коэффициент φ продольного изгиба
приводится в СНиП с учетом дополнительного запаса, обусловленного возможными
несовершенствами сжатого стержня. Чтобы убедиться в этом, рассмотрим,
например, стержень с условной гибкостью \( \overline{\lambda} > 4,5
\), для которого в СНиП II-23-81* приведена формула 10:
φ \( = 332/[ \overline{\lambda}_2 (51-\overline{\lambda})] \). Сопоставим
этот результат с решением Эйлера: σкр = π2Ry
/ \( \overline{\lambda}\)2.
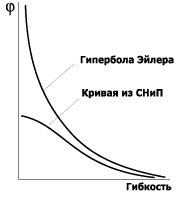
Зависимость
φ(λ) |
Для этого определим коэффициент запаса, равный σкр
/(φRy). Он меняется от 1,38 при \( \overline{\lambda}
\) = 4,5 до 1,10 при \( \overline{\lambda} \) = 14.
Необходимо также отметить, что при малых гибкостях сказывается
и еще одно различие — формулы норм учитывают пластическую
стадию работы материала при потере устойчивости, в то время
как комплекс дает решение задачи об устойчивости упругой системы.
В комплексе SCAD
учет пластичности не реализован по следующим причинам:
во-первых, неизвестно, что делать для элементов
из материалов, отличных от предусматриваемых нормами; во-вторых, неизвестно, интересует пользователя,
например, СНиП II-23-81* Стальные конструкции или СНиП
2.05.03-84 Мосты и трубы. В последнем документе даже для
стальных конструкций кривые φ(λ) — разные, поскольку
различны предположения о величине начальных несовершенств. |
Если вспомнить, что есть железобетонные, деревянные, пластмассовые и
всяческие другие конструкции, то учет всех тонкостей, связанных с их проверкой
по нормам, далеко уводит от универсальной
расчетной программы.
