Calculation of the Load-Bearing Capacity of a Bar Structural Member from a Cold-Formed Hat Channel under Axial Compression
Task: Verify the correctness of the calculation of the load-bearing capacity of bar structural members from cold-formed profiles under axial compression.
Source: [1] Worked examples according to EN 1993-1-3, Eurocode 3, Part 1-3 // ECCS TC7 TWG 7.5 Practical Improvement of Design Procedure. – 1st Ed., ECCS CECM, EKS, 2008. – 235 p.
Compliance with the codes: EN 1993-1-3.
Initial data file:
Task 4.2.sav; report – Report 4.2.doc
Program version: MAGNUM 23.1.1.3, 07.02.2024
Initial data:
| Е = 210000 N/mm2 | Elastic modulus |
| v = 0.3 | Poisson’s ratio |
| fy = 355 N/mm2 | Yield strength |
| γМ0 = 1 | Partial safety factor |
| γМ1 = 1 | Partial safety factor |
| h = 180 mm | Section height (along the outer edge) |
| b = 175 mm | Flange width (along the outer edge) |
| c = 95 mm | Flange bend length (along the outer edge) |
| t = 3 mm | Profile thickness (minus the coating thickness) |
| r = 3.5 mm | Fillet radius (inner) |
| N = 214.29 kN | Design axial force |
| ℓy = 316 cm | Effective length of the bar member with respect to the y-y axis |
| ℓz = 158 cm | Effective length of the bar member with respect to the z-z axis |
Results in MAGNUM:
Steel: S355
Importance factor 1
Effective length factor for torsional buckling:
coefficient to the geometric length = 1
Section
|
h = 175 mm |
Member length 3,16 м

Effective length factor in the XOY plane - 0,5

Effective length factor in the XOZ plane - 1
Type of moment diagram

Load position
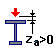
Height of the load application point = 0 mm
Length between restraints out of the bending plane:
geometric length factor = 1
Effective length factors depending on the boundary conditions of the support sections:
rotation out of the bending plane = 1
warping = 1
|
|
N |
My |
Vz |
Mz |
Vy |
T |
B |
Tw |
|---|---|---|---|---|---|---|---|---|
|
kN |
t*m |
kN |
t*m |
kN |
t*m |
kN*m2 |
t*m |
|
|
1 |
-214,29 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Comparison of solutions
|
Factor |
[1], p.181…184 |
MAGNUM, EN1993-1-1 |
% |
|---|---|---|---|
|
Strength of member |
– |
0,554 |
– |
|
Stability under axial compression (flexural buckling about the y-y axis) |
214,29/385,56 = 0,556 |
0,56 |
0,714 |
|
Stability under axial compression (flexural buckling about the z-z axis) |
214,29/421,83 = 0,508 |
0,491 |
3,34 |
|
Stability under axial compression (torsional and torsional-flexural buckling) |
214,29/214,29 = 1 |
1,113 |
11,3 |
Comments
When assessing the overall stability of a bar member in [1] the cross-sectional properties were calculated taking into account the fillets. In MAGNUM they are calculated without taking the fillets into account, which is permitted by the codes for the considered fillet radius (see Sec. 5.1(3) EN1993-1-3).
