Geometric Properties of a Closed Thin-walled Elliptical Section
Aim: To check the accuracy of the geometric properties calculation for a closed elliptical shell of the rod cross-section.
Name of a file with the initial data: Ellipse_Shell.tns
Formulation: Check the accuracy of the geometric properties calculation for a closed elliptical shell of the rod cross-section.
References: Umansky A. A., Reference book for designers of industrial, apartment and civil buildings (theoretical calculation). Book 1, Moscow, Publishing House On Construction, 1972.
Aleksandrov A.V., Potapov V.D., Derzhavin B.P., Strength of Materials, Moscow, Vysshaya shkola, 1995.
Initial data:
| a = 50 cm | - length of the semi-major axis of an elliptical shell of the cross-section (along Y axis); |
| b = 30 cm | - length of the semi-minor axis of an elliptical shell of the cross-section (along Z axis); |
| t = 1.0 cm | - thickness of the shell of the cross-section. |
Design model: The design model is created on the basis of a model of the central contour imported from the AutoCad graphic editor. The model of the contour is a polygon inscribed in an ellipse with given properties and built in polar coordinates with an angle step φ = 3°. The number of vertices of a polygon in a model is 120.
Results Obtained in Tonus
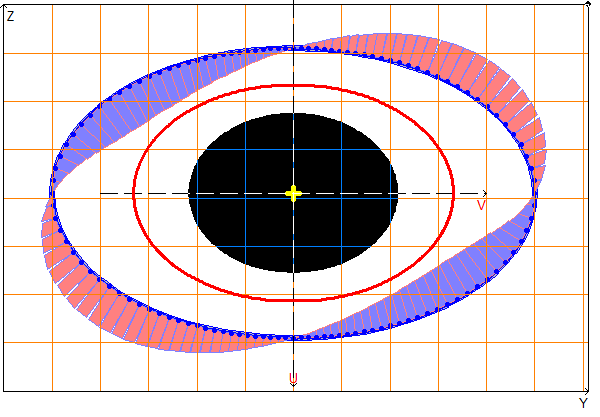
Design model, principal axes, center of mass, ellipse of inertia, core of the section, sectorial coordinate diagrams
Comparison of results:
|
Parameter |
Theory |
TONUS |
Deviation, % |
|---|---|---|---|
|
Cross-sectional area, A cm2 |
255.180 |
255.215 |
0.01 |
|
Conventional shear area along the principal U-axis, Av,y cm2 |
81.383 |
80.890 |
0.61 |
|
Conventional shear area along the principal V-axis, Av,z cm2 |
173.738 |
174.325 |
0.34 |
|
Angle of the principal axes of inertia, α rad |
1.5708 |
1.5708 |
0.00 |
|
Moment of inertia about the centroidal Y1 axis parallel to the coordinate Y axis, Iy cm4 |
128657.250 |
128839.668 |
0.14 |
|
Moment of inertia about the centroidal Z1 axis parallel to the coordinate Z axis, Iz cm4 |
280418.750 |
279824.429 |
0.21 |
|
Torsional moment of inertia, It cm4 |
348176.760 |
347677.226 |
0.14 |
|
Sectorial moment of inertia, Iw cm6 |
4265014.702 |
4260080.440 |
0.12 |
|
Radius of gyration about Y1 axis, iy cm |
22.457 |
22.468 |
0.05 |
|
Radius of gyration about Z1 axis, iz cm |
33.154 |
33.112 |
0.13 |
|
Maximum section modulus about U-axis, Wu+ cm3 |
5608.375 |
5541.222 |
1.20 |
|
Minimum section modulus about U-axis, Wu‒ cm3 |
5608.375 |
5541.222 |
1.20 |
|
Maximum section modulus about V-axis, Wv+ cm3 |
4288.575 |
4224.254 |
1.50 |
|
Minimum section modulus about V-axis, Wv‒ cm3 |
4288.575 |
4224.254 |
1.50 |
|
Plastic section modulus about U-axis, Wpl,u cm3 |
7471.878 |
7467.234 |
0.06 |
|
Plastic section modulus about V-axis, Wpl,v cm3 |
5277.357 |
5275.030 |
0.04 |
|
Maximum moment of inertia, Iu cm4 |
280418.750 |
279824.429 |
0.21 |
|
Minimum moment of inertia, Iv cm4 |
128657.250 |
128839.668 |
0.14 |
|
Maximum radius of gyration, iu cm |
33.154 |
33.112 |
0.13 |
|
Minimum radius of gyration, iv cm |
22.457 |
22.468 |
0.05 |
|
Core size along positive Y(U)-axis, a u+ cm |
16.810 |
16.552 |
1.53 |
|
Core size along negative Y(U)-axis, a u‒ сm |
16.810 |
16.552 |
1.53 |
|
Core size along positive Z(V)-axis, a v+ cm |
21.983 |
21.712 |
1.23 |
|
Core size along negative Z(V)-axis, a v‒ cm |
21.983 |
21.712 |
1.23 |
|
Y-coordinate of the center of mass, ym cm |
0.000 |
0.000 |
— |
|
Z-coordinate of the center of mass, zm cm |
0.000 |
0.000 |
— |
|
Y-coordinate of the shear center, yb cm |
0.000 |
0.013 |
— |
|
Z-coordinate of the shear center, zb cm |
0.000 |
0.040 |
— |
|
Perimeter, P cm |
510.360 |
510.430 |
0.01 |
|
Internal perimeter, Pi cm |
255.180 |
255.215 |
0.01 |
|
External perimeter, Pe cm |
255.180 |
255.215 |
0.01 |
|
Polar moment of inertia, Ip cm4 |
409076.000 |
408664.097 |
0.10 |
|
Polar radius of gyration, ip cm |
40.043 |
40.016 |
0.07 |
|
Polar section modulus, Wp cm3 |
8181.520 |
8092.567 |
1.09 |
Values of sectorial coordinates ω in the first quarter of the Cartesian coordinate system UV, cm2
|
φ, ° |
Theory |
TONUS |
Deviation, % |
|---|---|---|---|
|
0 |
0.000 |
0.000 |
0.00 |
|
3 |
-33.798 |
-33.931 |
0.39 |
|
6 |
-66.041 |
-66.277 |
0.36 |
|
9 |
-95.381 |
-95.675 |
0.31 |
|
12 |
-120.827 |
-121.132 |
0.25 |
|
15 |
-141.807 |
-142.088 |
0.20 |
|
18 |
-158.147 |
-158.383 |
0.15 |
|
21 |
-169.998 |
-170.171 |
0.11 |
|
24 |
-177.691 |
-177.821 |
0.07 |
|
27 |
-181.736 |
-181.819 |
0.05 |
|
30 |
-182.648 |
-182.691 |
0.02 |
|
33 |
-180.947 |
-180.957 |
0.01 |
|
36 |
-177.108 |
-177.094 |
0.01 |
|
39 |
-171.555 |
-171.521 |
0.02 |
|
42 |
-164.646 |
-164.598 |
0.03 |
|
45 |
-156.680 |
-156.624 |
0.04 |
|
48 |
-147.904 |
-147.842 |
0.04 |
|
51 |
-138.514 |
-138.448 |
0.05 |
|
54 |
-128.666 |
-128.599 |
0.05 |
|
57 |
-118.482 |
-118.417 |
0.05 |
|
60 |
-108.058 |
-107.995 |
0.06 |
|
63 |
-97.466 |
-97.407 |
0.06 |
|
66 |
-86.761 |
-86.706 |
0.06 |
|
69 |
-75.982 |
-75.933 |
0.06 |
|
72 |
-65.158 |
-65.115 |
0.07 |
|
75 |
-54.310 |
-54.273 |
0.07 |
|
78 |
-43.450 |
-43.420 |
0.07 |
|
81 |
-32.586 |
-32.564 |
0.07 |
|
84 |
-21.722 |
-21.707 |
0.07 |
|
87 |
-10.861 |
-10.853 |
0.07 |
|
90 |
0.000 |
0.000 |
0.00 |
Notes: Geometric properties of the closed elliptical shell of the rod cross-section can be determined analytically by the following formulas:
\[ A=4\cdot t\cdot a\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right); \] \[ A_{v,y} =4\cdot t\cdot \frac{a\cdot b^{2}}{a^{2}-b^{2}}\cdot \left[ {F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)-E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right]; \] \[ A_{v,z} =4\cdot t\cdot \frac{a}{a^{2}-b^{2}}\cdot \left[ {a^{2}\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)-b^{2}\cdot F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right]; \] \[ \alpha =0; \] \[ \mbox{I}_{\mbox{y}} =I_{v} =I_{1} =\frac{4}{3}\cdot t\cdot \frac{a\cdot b^{2}}{a^{2}-b^{2}}\cdot \left[ {\left( {2\cdot a^{2}-b^{2}} \right)\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)-b^{2}\cdot F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right]; \] \[ \mbox{I}_{\mbox{z}} =I_{u} =I_{2} =\frac{4}{3}\cdot t\cdot \frac{a^{3}}{a^{2}-b^{2}}\cdot \left[ {\left( {a^{2}-2\cdot b^{2}} \right)\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)+b^{2}\cdot F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right]; \] \[ I_{t} =\frac{\pi^{2}\cdot t\cdot a\cdot b^{2}}{E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}; \] \[ \omega =a\cdot b\cdot \left[ {\arcsin \left( {\frac{v}{a}} \right)-\frac{\pi }{2}\cdot \frac{E\left( {\arcsin \left( {\frac{v}{a}} \right);\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}{E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}} \right]; \] \[ v=\frac{a\cdot b\cdot \cos \left( \phi \right)}{\sqrt {a^{2}\cdot \sin ^{2}\left( \phi \right)-b^{2}\cdot \cos^{2}\left( \phi \right)} }; \] \[ {\begin{array}{*{20}c} {I_{\omega } \approx \frac{\pi^{2}\cdot t\cdot a^{3}\cdot b^{2}}{E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}\cdot \left[ {0.007812500\cdot \frac{\left( {a^{2}-b^{2}} \right)^{2}}{a^{4}}+0.003906250\cdot \frac{\left( {a^{2}-b^{2}} \right)^{3}}{a^{6}}+} \right.} \\ {+0.002326965\cdot \frac{\left( {a^{2}-b^{2}} \right)^{4}}{a^{8}}+0.001537323\cdot \frac{\left( {a^{2}-b^{2}} \right)^{5}}{a^{10}}+0.001087957\cdot \frac{\left( {a^{2}-b^{2}} \right)^{6}}{a^{12}}+} \\ {+0.000808729\cdot \frac{\left( {a^{2}-b^{2}} \right)^{7}}{a^{14}}+0.000254599\cdot \frac{\left( {a^{2}-b^{2}} \right)^{8}}{a^{16}}+0.000113341\cdot \frac{\left( {a^{2}-b^{2}} \right)^{9}}{a^{18}}+} \\ {\left. {+0.000053772\cdot \frac{\left( {a^{2}-b^{2}} \right)^{10}}{a^{20}}+0.000024374\cdot \frac{\left( {a^{2}-b^{2}} \right)^{11}}{a^{22}}+0.000008701\cdot \frac{\left( {a^{2}-b^{2}} \right)^{12}}{a^{24}}} \right]} \\ \end{array} }; \] \[ i_{y} =i_{v} =\sqrt {\frac{b^{2}}{3\cdot \left( {a^{2}-b^{2}} \right)}\cdot \left\{ {2\cdot a^{2}-b^{2}\cdot \left[ {1+\frac{F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}{E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}} \right]} \right\}} ; \] \[ i_{z} =i_{u} =\sqrt {\frac{a^{2}}{3\cdot \left( {a^{2}-b^{2}} \right)}\cdot \left\{ {a^{2}-2\cdot b^{2}\cdot \left[ {1-\frac{F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}{2\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}} \right]} \right\}} ; \] \[ W_{u+} =W_{u-} =\frac{4}{3}\cdot t\cdot \frac{a^{2}}{a^{2}-b^{2}}\cdot \left[ {\left( {a^{2}-2\cdot b^{2}} \right)\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)+b^{2}\cdot F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right]; \] \[ W_{v+} =W_{v-} =\frac{4}{3}\cdot t\cdot \frac{a\cdot b}{a^{2}-b^{2}}\cdot \left[ {\left( {2\cdot a^{2}-b^{2}} \right)\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)-b^{2}\cdot F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right]; \] \[ W_{pl,u} =2\cdot t\cdot a\cdot \left[ {a+\frac{b^{2}}{\sqrt {a^{2}-b^{2}} }\cdot \ln \left| {\frac{\sqrt {a^{2}-b^{2}} +a}{b}} \right|} \right]; \] \[ W_{pl,v} =2\cdot t\cdot b\cdot \left[ {b+\frac{a^{2}}{\sqrt {a^{2}-b^{2}} }\cdot \arcsin \left( {\frac{\sqrt {a^{2}-b^{2}} }{b}} \right)} \right]; \] \[ a_{u+} =a_{u-} =\frac{1}{3}\cdot \frac{b}{a^{2}-b^{2}}\cdot \left\{ {2\cdot a^{2}-b^{2}\cdot \left[ {1+\frac{F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}{E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}} \right]} \right\}; \] \[ a_{v+} =a_{v-} =\frac{1}{3}\cdot \frac{a}{a^{2}-b^{2}}\cdot \left\{ {a^{2}-2\cdot b^{2}\cdot \left[ {1-\frac{F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}{2\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}} \right]} \right\}; \] \[ y_{m} =y_{b} =z_{m} =z_{b} =0; \] \[ P_{e} =P_{i} =4\cdot a\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right); \quad P=P_{e} +P_{i} ; \] \[ I_{12} =0; \] \[ I_{p} =\frac{4}{3}\cdot t\cdot a\cdot \left[ {\left( {a^{2}+b^{2}} \right)\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)+b^{2}\cdot F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right]; \] \[ i_{p} =\sqrt {\frac{1}{3}\cdot \left\{ {a^{2}+b^{2}\cdot \left[ {1+\frac{F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}{E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)}} \right]} \right\}} ; \] \[ W_{p} =\frac{4}{3}\cdot t\cdot \left[ {\left( {a^{2}+b^{2}} \right)\cdot E\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)+b^{2}\cdot F\left( {\frac{\sqrt {a^{2}-b^{2}} }{a}} \right)} \right], \]
where: F(x) – Legendre complete elliptic integral of the first kind,
E(x) – Legendre complete elliptic integral of the second kind,
E(k,x) Legendre incomplete elliptic integral of the second kind.