Sectorial Properties of an I-beam with Unequal Flanges

Aim: To check the accuracy of the geometric properties calculation for a thin-walled I-beam with unequal flanges.

Name of a file with the initial data: ISection.tns

Formulation: Check the accuracy of the geometric properties calculation for a rod cross-section in the form of a thin-walled I-beam with unequal flanges.

References: Young W.C., Budynas R.G., Roark's Formulas for Stress and Strain, New York , McGraw-Hill,  New York, 2002.
Umansky A. A., Reference book for designers of industrial, apartment and civil buildings (theoretical calculation). Book 1, Moscow, Publishing House On Construction, 1972.

Initial data:

Geometric dimensions of the section:

b1 = 100 cm,

b2 = 60 cm,

h = 120 cm,

t1 = 3 cm,

t2 = 2 cm,

tw = 4 cm.

Results Obtained in Tonus:

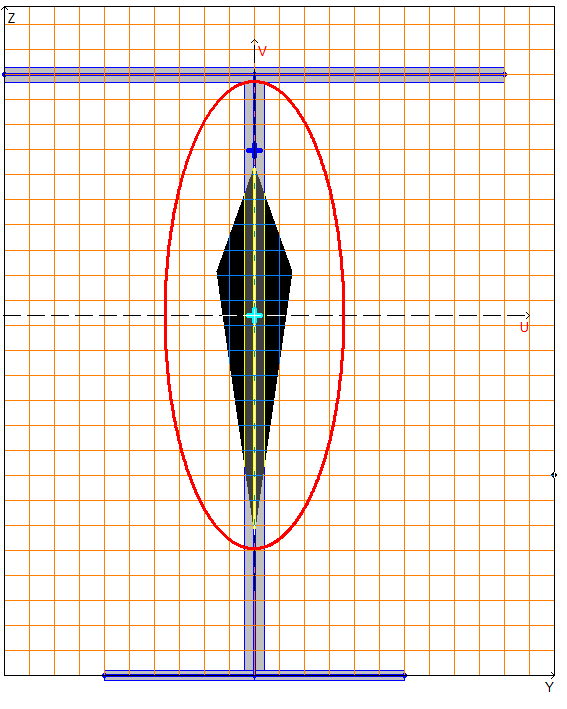
Design model, coordinate and principal axes, center of mass, ellipse of inertia, core of the section

Comparison of results:

Parameter	Theory	TONUS	Deviation, %
Cross-sectional area, A cm2	900	900	0
Conventional shear area along the principal U-axis, Av,y cm2	420	420	0
Conventional shear area along the principal V-axis, Av,z cm2	480	480	0
Torsional moment of inertia, It cm4	3620	3620	0
Sectorial moment of inertia, Iw cm6	453146853,147	453146853,147	0
Y-coordinate of the shear center, yb cm	50	50	0
Z-coordinate of the shear center, zb cm	104,895	104,895	0

Notes: Geometric properties can be determined analytically by the following formulas:

\[ A=t_{1} b_{1} +t_{2} b_{2} +t_{w} h; \] \[ A_{v,y} =t_{1} b_{1} +t_{2} b_{2} ; \] \[ A_{v,z} =t_{w} h; \] \[ I_{t} =\frac{1}{3}\left( {t_{1}^{3} b_{1} +t_{2}^{3} b_{2} +t_{w}^{3} h} \right); \] \[ I_{\omega } =\frac{h^{2}t_{1} t_{2} b_{1}^{3} b_{2}^{3} }{12\left( {t_{1} b_{1}^{3} +t_{2} b_{2}^{3} } \right)}; \] \[ e=\frac{t_{1} b_{1}^{3} h}{t_{1} b_{1}^{3} +t_{2} b_{2}^{3} }. \]