Sectorial Properties of a Thin-walled Ring Sector

Aim: To check the accuracy of the geometric properties calculation for a thin-walled ring sector.

Name of a file with the initial data: ArcSection.tns

Formulation: Check the accuracy of the geometric properties calculation for a thin-walled rod cross-section in the form of a ring sector.

References: Young W.C., Budynas R.G., Roark's Formulas for Stress and Strain, New York , McGraw-Hill, New York, 2002.

Initial data:

Geometric dimensions of the section:

r = 100 cm,

t = 3 cm,

α= 67,5°.

Design model: The design model is created on the basis of a model of the central contour. The model of the contour is a polygon inscribed in an arc of a circle with specified properties. The number of vertices of a polygon in a model is 24.

Results Obtained in Tonus:

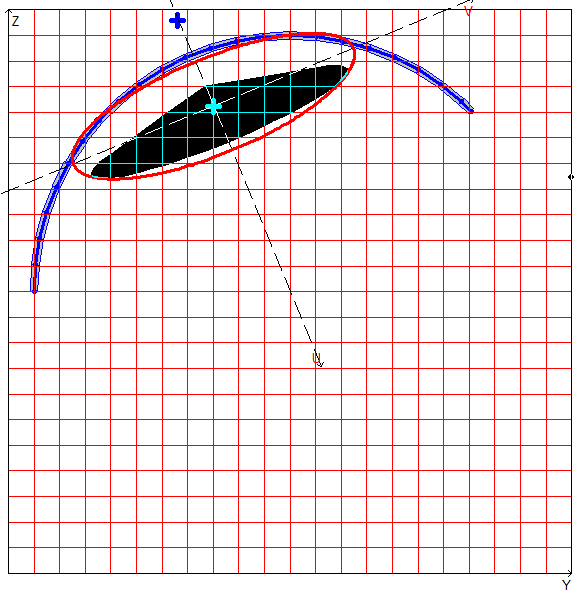
Design model, coordinate and principal axes, center of mass, ellipse of inertia, core of the section

Comparison of results:

Parameter	Theory	TONUS	Deviation, %
Cross-sectional area, A сm²	706,858	707,159	0,043
Conventional shear area along the principal U-axis, A_v,y cm²	247,313	247,879	0,229
Conventional shear area along the principal V-axis, A_v,z cm²	459,487	459,279	0,045
Torsional moment of inertia, I_t cm⁴	2126,858	2121,476	0,253
Sectorial moment of inertia, I_w cm⁶	135771063,361	136173663,259	0,297
Y-coordinate of the shear center, y_b cm	66,229	66,232	0,005
Z-coordinate of the shear center, z_b cm	215,963	215,981	0,008

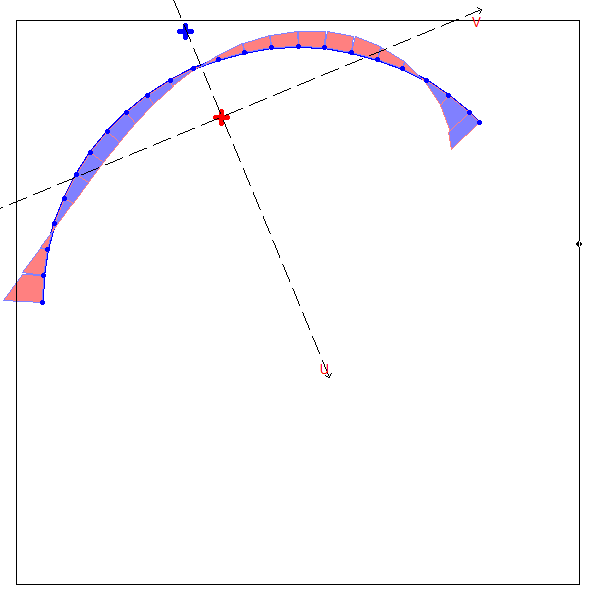
Sectorial Coordinate Diagrams

Notes: Geometric properties can be determined analytically by the following formulas:

\[ A=r\alpha ; \] \[ A_{v,y} =2rt\left( {\frac{\alpha }{2}-\frac{\sin (2\alpha )}{4}} \right); \] \[ A_{v,z} =2rt\left( {\frac{\alpha }{2}+\frac{\sin (2\alpha )}{4}} \right); \] \[ I_{t} =\frac{2}{3}t^{3}r\alpha ; \] \[ I_{\omega } =\frac{2tr^{5}}{3}\left[ {\alpha^{3}-6\frac{(\sin \alpha -\alpha \cos \alpha )^{2}}{\alpha -\sin \alpha \cos \alpha }} \right]; \] \[ e=2r\frac{\sin \alpha -\alpha \cos \alpha }{\alpha -\sin \alpha \cos \alpha }. \]