Sectorial Areas, Static Moments, and Tangential Stresses for an Open Thin-Walled Section
Aim: To check the accuracy of the determination of sectorial areas ω, a sectorial static moment Sω, and tangential stresses τω, caused by constrained torsion for an open thin-walled section.
Name of a file with the initial data: Prokic_open.tns
Formulation: Check the accuracy of the calculation of the sectorial areas, static moments, and tangential stresses for an open thin-walled section.
References: Prokić A. Computer program for determination of geometrical properties of thin-walled beams with open-closed section // Computers and Structures, Vol. 74 (2000). – pp. 705 – 715.
Initial data:
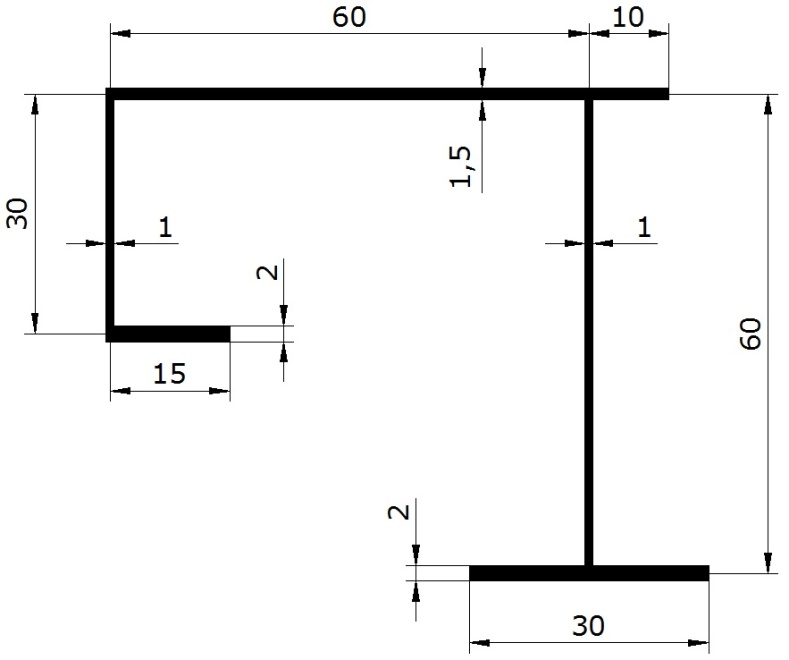
Open thin-walled section with sizes, cm
Results from the source:
 |
 |
|
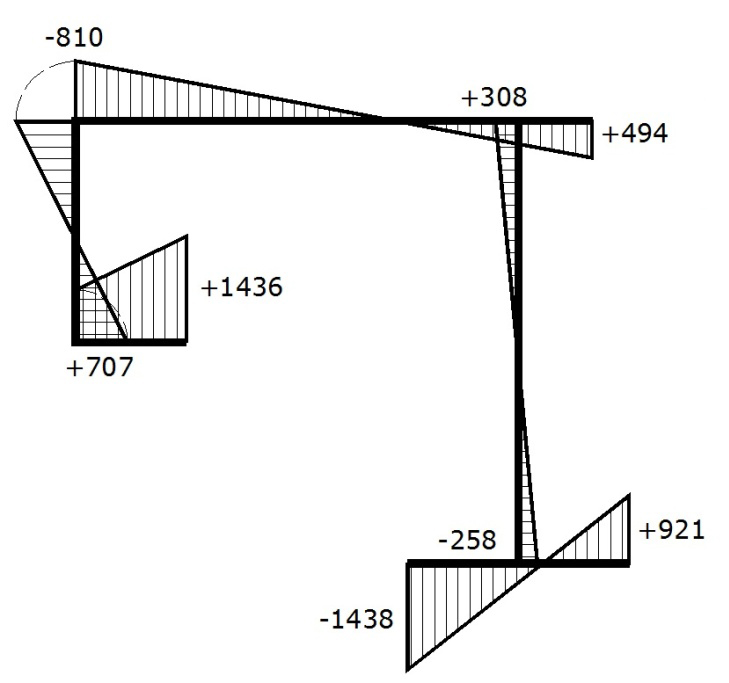
Sectorial area diagram ω, cm2
|
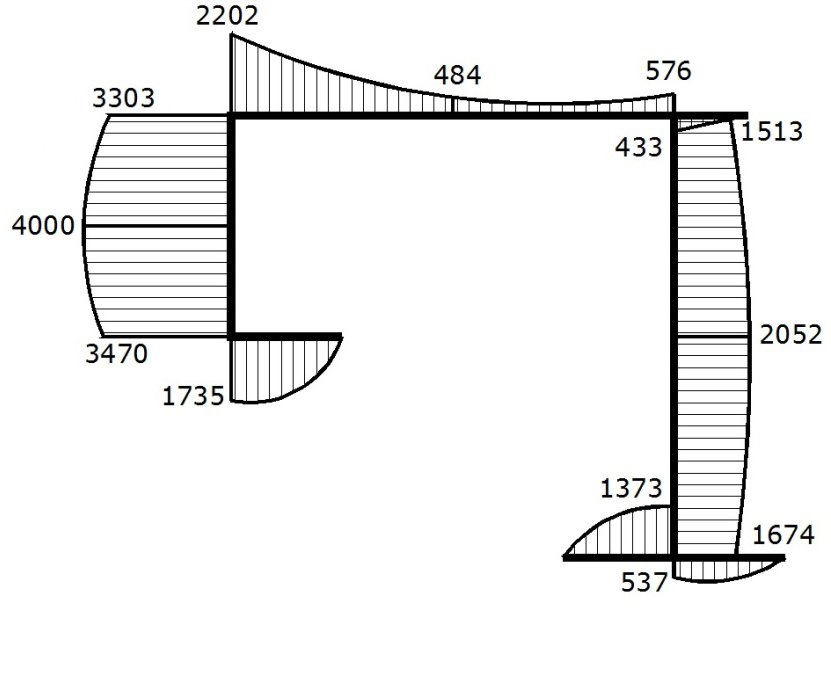
Diagram of tangential stresses related to the constrained torque, τω/Mω×107, 1/cm3 |
Results obtained in Tonus:
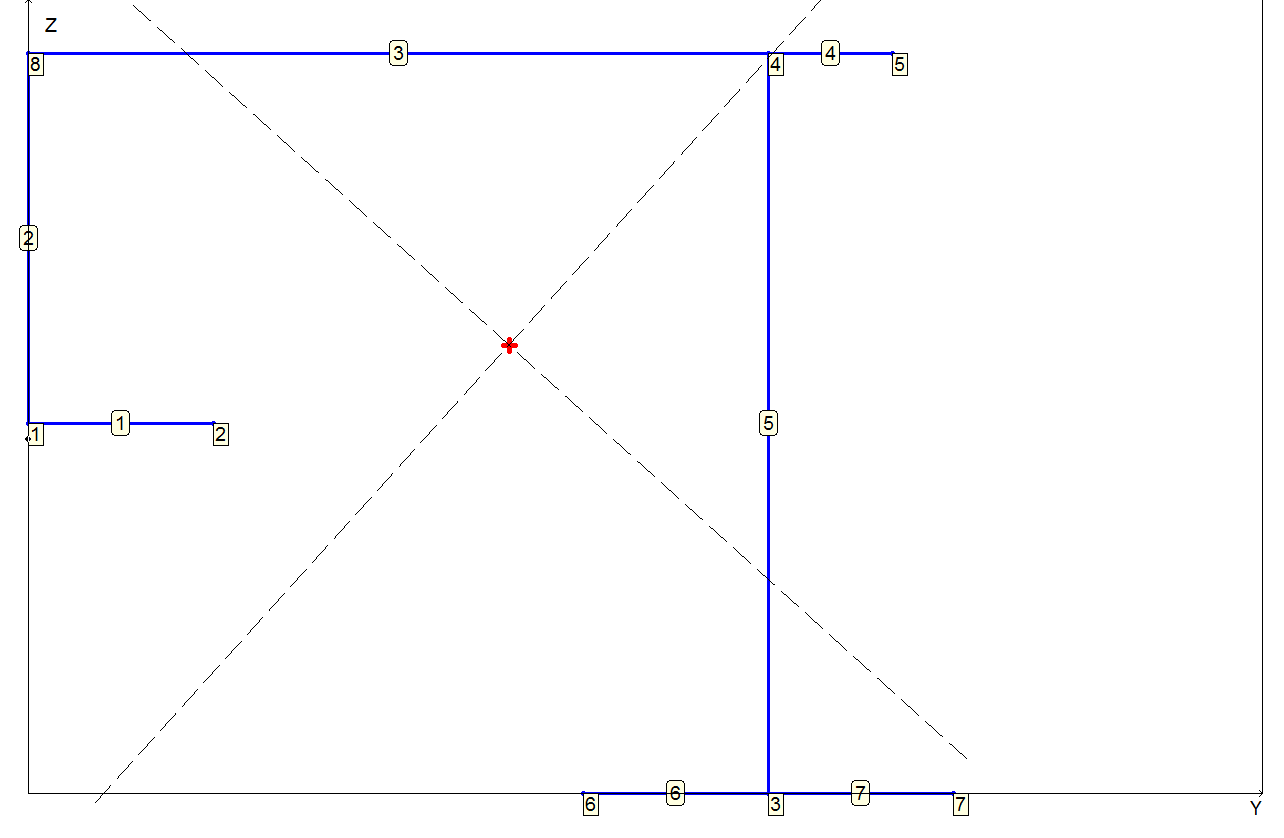
Numbering of vertices and strips, position of the mass center and shear center
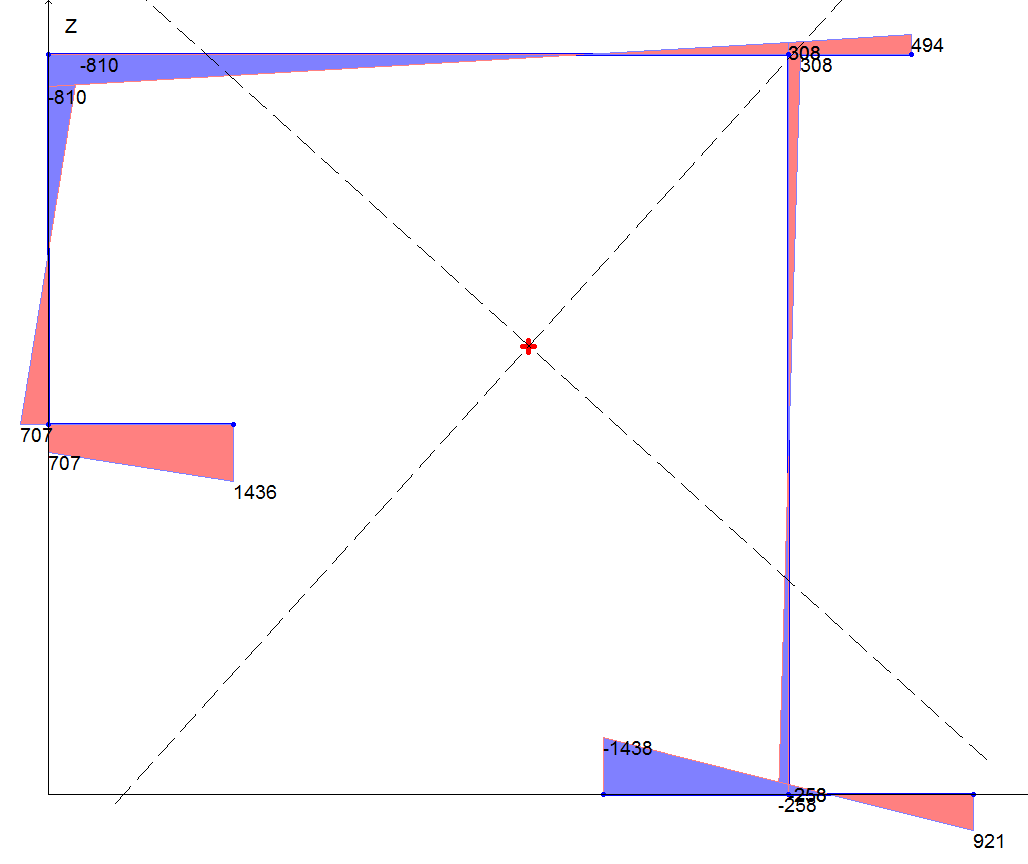
Sectorial area diagram ω, cm2
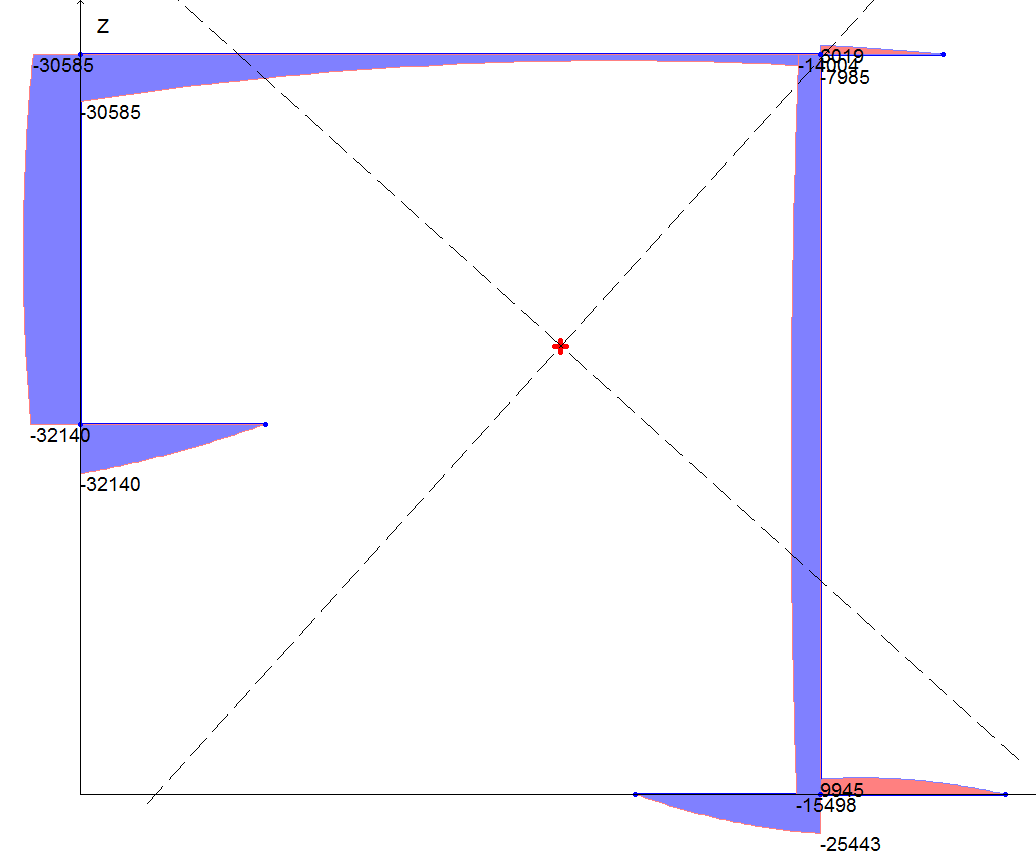
Sectorial static moment diagram Sω, cm4
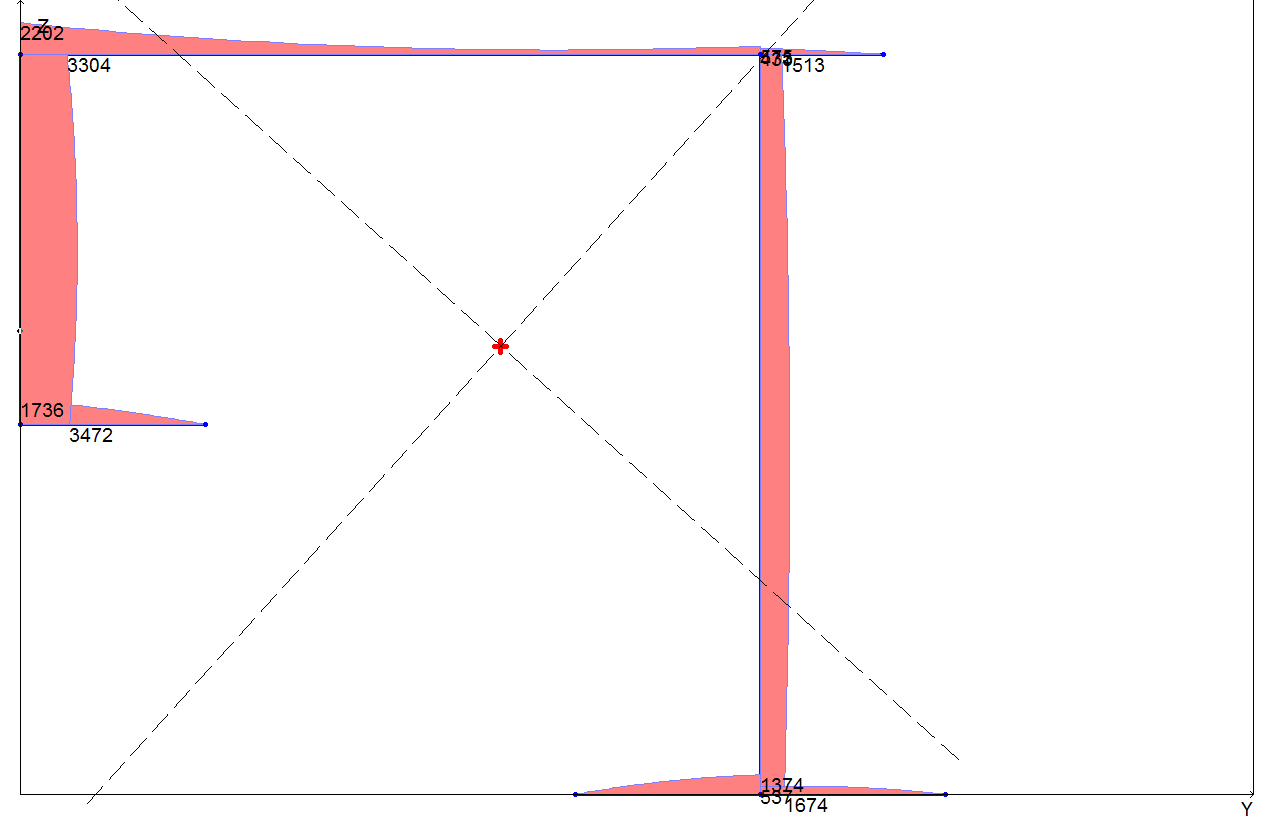
Diagram of the tangential stress module τω for the value of the constrained torque Mω = 107, kNcm
Comparison of results:
|
Element number |
Vertex number |
Sectorial static moment, cm4 |
Tangential stress, kN/cm2 (at Mω = 107, kNcm) |
||||
|---|---|---|---|---|---|---|---|
|
Source* |
TONUS |
Deviation, % |
Source |
TONUS |
Deviation, % |
||
|
1 |
1 |
32126 |
32140 |
0,04 |
1735 |
1736 |
0,06 |
|
1 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
|
2 |
1 |
32126 |
32140 |
0,04 |
3470 |
3472 |
0,06 |
|
2 |
8 |
30580 |
30585 |
0,02 |
3303 |
3304 |
0,06 |
|
3 |
8 |
30580 |
30585 |
0,02 |
2202 |
2202 |
0 |
|
3 |
4 |
7999 |
7985 |
0,18 |
576 |
575 |
0,17 |
|
4 |
4 |
6013 |
6019 |
0,1 |
433 |
432 |
0,23 |
|
4 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
4 |
14008 |
14004 |
0,03 |
1513 |
1513 |
0 |
|
5 |
3 |
15498 |
15498 |
0 |
1674 |
1674 |
0 |
|
6 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
|
6 |
3 |
25423 |
25443 |
0,08 |
1373 |
1374 |
0,07 |
|
7 |
3 |
9943 |
9945 |
0,02 |
537 |
537 |
0 |
|
7 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Note: *The value of the static sectorial moment Sω was calculated using the value τω/Mω, obtained from the source as (Iω = 92582119 cm6): Sω.= τωIωt / Mω. |
|||||||
|
Vertex number |
Sectorial area, cm2 |
||
|---|---|---|---|
|
Source |
TONUS |
Deviation, % |
|
|
1 |
707 |
707 |
0 |
|
2 |
1436 |
1436 |
0 |
|
3 |
-258 |
-258 |
0 |
|
4 |
308 |
308 |
0 |
|
5 |
494 |
494 |
0 |
|
6 |
-1438 |
-1438 |
0 |
|
7 |
921 |
921 |
0 |
|
8 |
-810 |
-810 |
0 |